Brandon Zhang
July 19, 2021
[BIC] Push-pull Feedback Implements Hierarchical Information Retrieval Efficiently
Liu, Xiao, et al. “Push-pull feedback implements hierarchical information retrieval efficiently.” Advances in Neural Information Processing Systems 32 (2019): 5701-5710.
Front Word
To understand this paper, you need a strong neuroscience background, especially knowing the Hopfield model and Hebbian theory. So before reading this paper, please preview the theories mentioned above!
To be honest, I still cannot understand the details quite well LoL :)
Abstract
- In addition to feedforward connections, there exist abundant feedback connections in a neural pathway.
- This paper investigate the role of feedback in hierarchical information retrieval.
- a hierarchical network storing the hierarchical categorical information of objects:
- Mechanism: information retrieval goes from rough to fine, aided by dynamical push-pull feedback from higher to lower layers.
- Function: 我们阐明，最佳反馈应该是动态的，随着时间的推移从正（推）到负（拉）而变化，它们分别抑制了来自不同类别和相同类别的模式关联所带来的干扰。
Gilad等人发现猴子在执行从复杂背景中检测边界时，初级视皮层（V1）的神经元群体先在早期出现增长，表现出“push”现象，而在后期减弱，表现出“pull”的现象（如图A所示）。这种现象被称为push-pull现象。
神经系统面临一个两难问题：一方面，为了对物体之间的层级类别关系进行编码，神经系统需要关联的神经表征；另一方面，为了可靠地检索信息，又需要克服这些相关性带来的计算噪声。在神经网络中如何实现可靠的关联信息检索是一个没有解决的问题。
A model for Hierarchical Information Representation
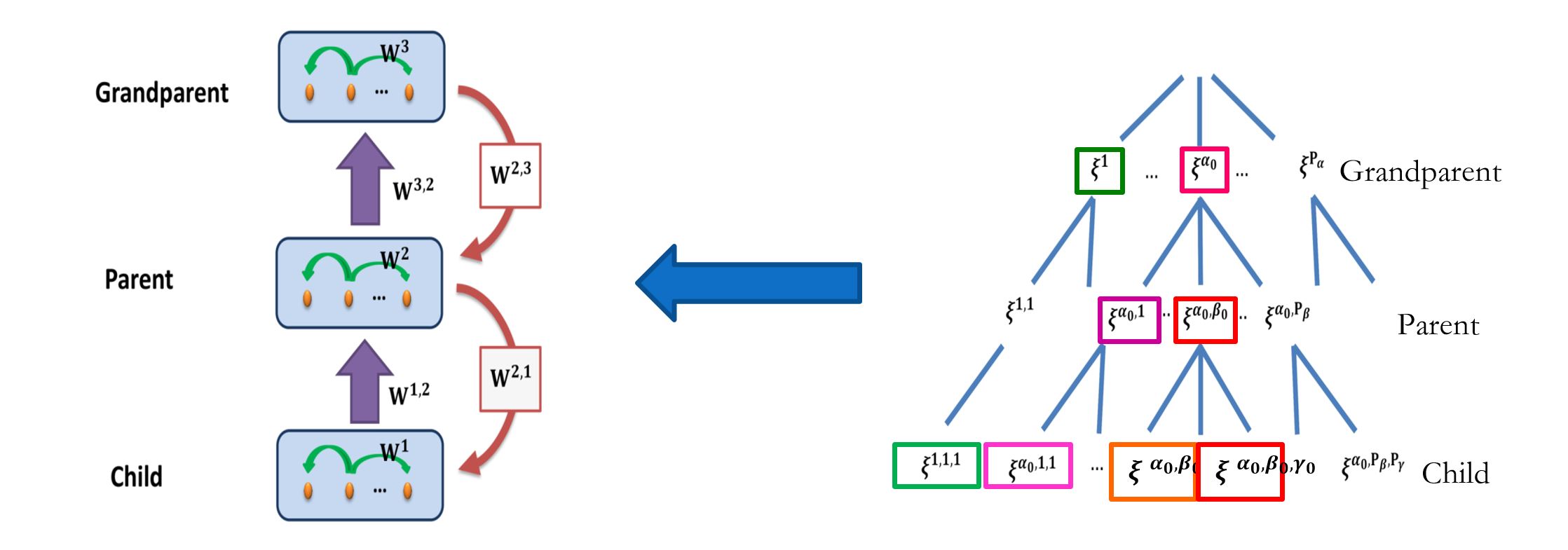
The model consists of three layers which store three-level of hierarchical memory patterns. From button to top, we call the three layers:
- Child layer
- Parent layer
- Grandparent layer
Neurons in the same layer are connected recurrently with each other to function as an associative memory. Between layers, neurons communicate via feedforward and feedback connections.
- $x_i^l(t)$: the state of neuron $i$ in layer $l$ at time $t$. value takes $\pm 1$.
- $W_{ij}^{l}$: symmetric recurrent connections from neuron $j$ to $i$ in layer $l$.
- $W_{ij}^{l+1, l}$: the **feedforward connections** from neuron $j$ of layer $l$ to neuron $i$ in layer $l + 1$.
- $W_{ij}^{l, l+1}$: the **feedback connections** from neuron $j$ of layer $l + 1$ to neuron $i$ of layer $l$.
There are 3 layers in this model, and each layer has $N$ neurons. The neuronal dynamics follows the Hopfield model, which is written as $$ x_i^l(t+1) = sign[h_i^l(t)]. $$ $h_i^l(t)$ is the total input received by the neuron. Using layer 1 as an example, we could have $$ h_i^l(t) = \sum_j W_{ij}^1 x_j^1(t) + W_{ij}^{1,2}x_j^2(t). $$
According to the figure above, $\xi$ means memory pattern, and we can construct weight based on these patterns:
- recurrent connections: $$W_{ij}^1 = \sum_{\alpha, \beta, \gamma} \xi_i^{\alpha,\beta,\gamma} \xi_j^{\alpha,\beta,\gamma} / N,$$ $$W_{ij}^2 = \sum_{\alpha, \beta} \xi_i^{\alpha,\beta} \xi_j^{\alpha,\beta} / N,$$ $$W_{ij}^3 = \sum_{\alpha} \xi_i^{\alpha} \xi_j^{\alpha} / N.$$
- feedforward connections: $$W_{ij}^{2,1} = \sum_{\alpha, \beta, \gamma} \xi_i^{\alpha,\beta} \xi_j^{\alpha,\beta,\gamma} / N,$$ $$W_{ij}^{3,2} = \sum_{\alpha, \beta} \xi_i^{\alpha} \xi_j^{\alpha,\beta} / N.$$
To quantify the retrieval performance, we define $m(t)$ to measure the overlap between neural state and memory pattern. $$ m^{\alpha,\beta,\gamma}(t) = \frac{1}{N} \sum_{i=1}^N \xi_i^{\alpha,\beta,\gamma} x_i^1(t), $$ where $-1 \lt m^{\alpha,\beta,\gamma}(t) \lt 1$ represents the retrieval accuracy of the memory pattern $\xi^{\alpha,\beta,\gamma}$.