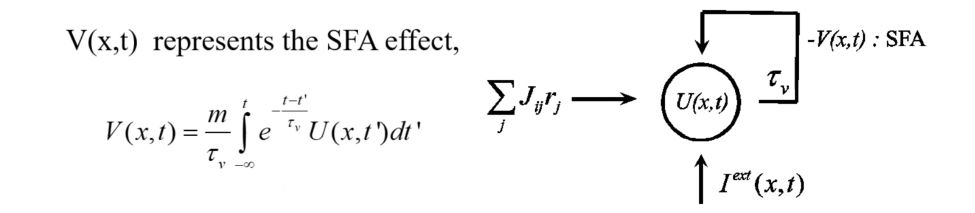[CN] Continuous-attractor Neural Network

Si Wu, Kosuke Hamaguchi, and Shun-ichi Amari. “Dynamics and computation of continuous attractors.” Neural computation 20.4 (2008): 994-1025.

本篇参考吴思老师公众号的文章《【学术思想】连续吸引子神经网络：神经信息表达的正则化网络模型》，并根据冷泉港亚洲暑期学校的讲座和智源学术沙龙的报告来详细阐释CANN的工作原理，全文用中文行文。

连续吸引子神经网络的数学模型

吸引子指的是一个动力学系统在不接受外界输入情况下靠自身动力学就能维持的非静息的稳定状态（active stationary state）。要构成一个的吸引子网络，需要两个基本条件：

神经元之间有兴奋性的互馈连接 (recurrent connection)，这样在没有外界输入的情况下，靠神经元之间的正反馈，网络就能维持住稳定活动；同时我们也要求兴奋性连接是局部的，这样才能形成有意义的空间局部活动；
网络中要有抑制性作用，这样才能避免系统活动因反复的正反馈而爆炸。

Hopfield模型采用吸引子的思想解释了大脑在收到部分或模糊信息条件下的联想式记忆机制。但经典的Hopfield模型没有考虑神经元之间连接的对称结构，因而其具有的吸引子（多个）在空间上是相互孤立的。

在吸引子网络的基础上，如果我们进一步要求神经元之间的连接具有空间平移不变性的对称结构，这时网络就将具有一簇连续的、而不是孤立的吸引子（注意，考虑到真实生物系统的神经数目足够大，为了方便，后面讨论都假设神经元数目是无穷的）；这些吸引子在参数空间上紧密排列，构成一个连续的状态子空间。

一维CANN数学模型

神经元的突触总输入$u$的动力学方程如下： $$ \tau \, \frac{du(x, t)}{dt} = -u(x,t) + \rho \int dx' J(x,x')\, r(x',t) + I_{ext} $$ 其中$x$表示神经元的参数空间位点，$u(x)$代表在参数空间位点x上的神经元的突触总输入，$r(x^′,t)$为神经元($x'$)的发放率，由以下公式给出: $$ r(x,t) = \frac{u(x,t)^2}{1+k\rho\int{dx’u(x',t)^2}} $$ 该模型没有单独考虑抑制性神经元，而是将其作用效果包含在除法归一化作用中。而神经元($x$)和($x'$)之间的兴奋性连接强度$J(x, x')$由高斯函数给出: $$ J(X,x') = \frac{1}{\sqrt{2\pi} \alpha} \, exp\left( - \frac{|x-x'|^2}{2\alpha^2}\right) $$ 我们看到其具有平移不变性，即其为$(x-x’)$的函数。外界输入$I_{ext}$与位置$z(t)$有关，公式如下： $$ I_{ext}=A \, exp \left[ - \frac{|x-z(t)|^2}{4\alpha^2}\right] $$

这个模型在数学上有精准解，使得我们可以对其动力学做细致的理论分析，从而更容易理解其计算功能，并将其用于神经建模中。

CANN的动力学性质

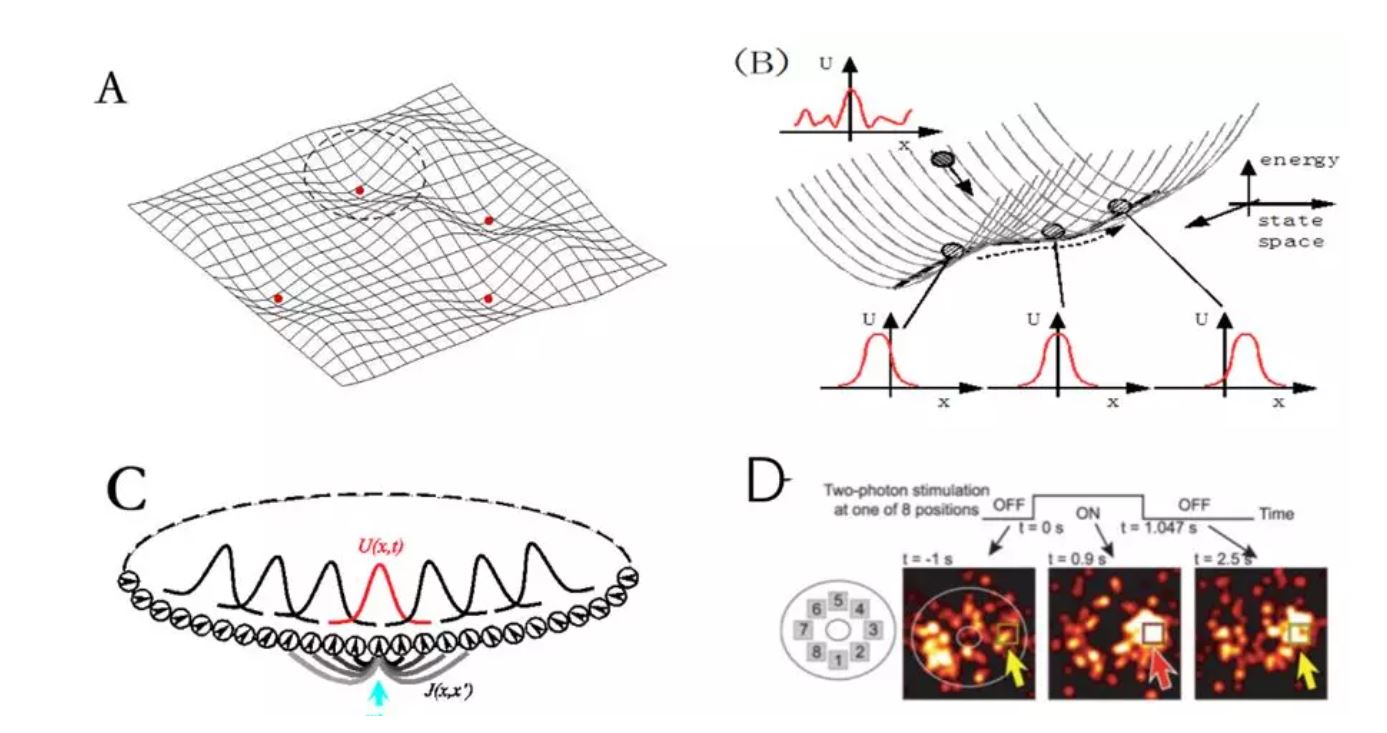
考虑一维参数空间x是一个周期变量，如朝向、运动方向、头朝向等。一个一维的CANN具有一簇高斯波包的稳定状态（图1C），它们在系统状态空间中构成一个一维的能量平滑的子空间（近似）（图1B）。在这个子空间上，因为能量函数是平的，系统状态处于随遇平衡(neutral stability)；这意味着在外部微小输入的驱动下，系统可以轻松改变状态。注意这个性质是其它非连续吸引子网络（如Hopfield网络）所不具有的（图1A）。这个随遇平衡是CANN动力学的关键，它使得网络状态能够平滑跟踪外部运动输入，从而实现了多项计算功能，如编码头朝向编码和空间位置等。

CANN的计算性质

1. 神经元群编码

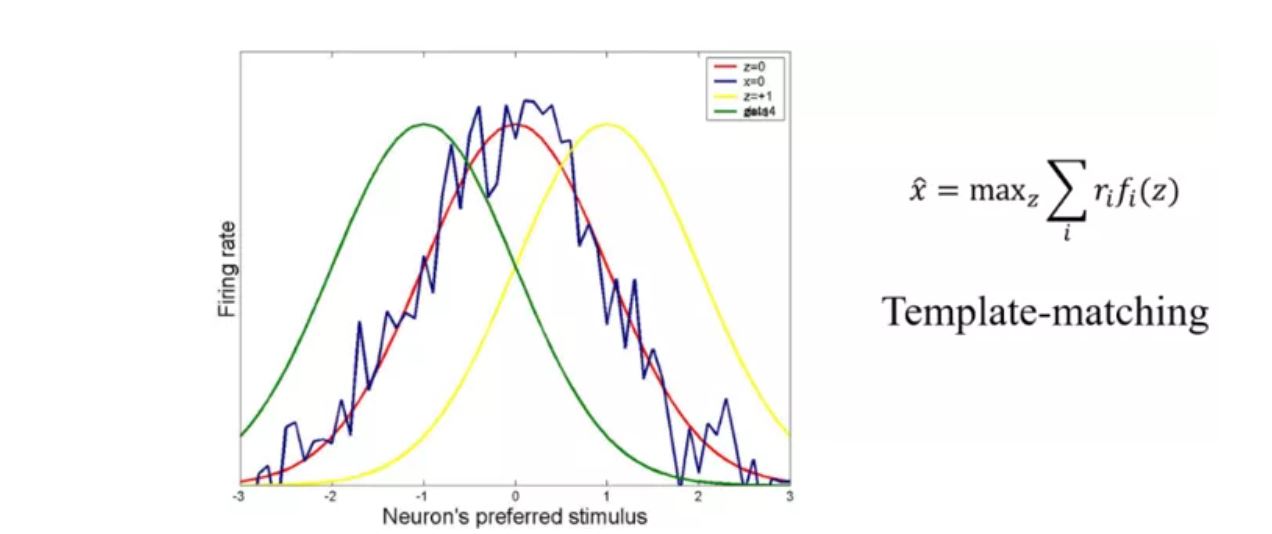
实验发现，对于很多类型的刺激，尤其是连续变量（如角度、空间位置等），神经系统的编码策略为：一大群神经元共同协作编码刺激值，其中每个神经元的反应覆盖一定范围的刺激值，且对某个特定值产生最大反应（表现为高斯形状的调谐函数）；神经元群的调谐函数覆盖整个参数空间。

CANN实现优化的神经元群编码。在接受外部有噪声的输入后，网络状态（波包）会快速移动到一个位置，使得波包和噪声输入的重叠最大，相当于一个template matching的操作，波包的顶点位置即为解码结果。

2、预测跟踪

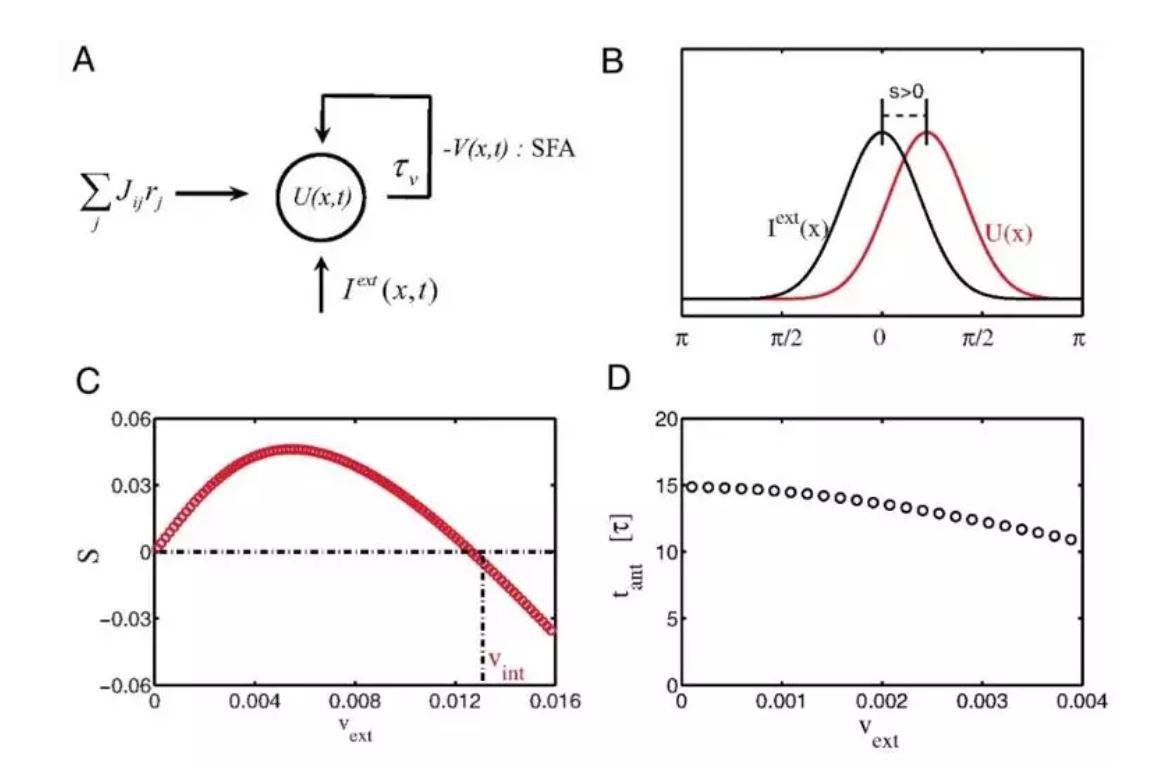
为了实现预测跟踪，我们研究发现，如果在神经元动力学中引入神经系统广泛存在的负反馈机制（其可以是单个神经元发放强度的自适应（spike frequency adaptation）（图5A）、神经元之间突触的短时程衰减(short-term plasticity)、或者不同层间的反馈抑制等），那么CANN就可以实现时间上恒定领先的运动预测跟踪（图5B）。我们首先发现在引入互反馈机制后，CANN能维持一个行波解(travelling wave)，且行波的速度（网络的内在速度）由负反馈强度调制。在接受运动输入的情况下，网络中波包移动速度被锁定到输入的运动速度，但其空间位置是领先还是落后于目标位置则是由网络内在速度与目标运动速度的相对大小来决定的（图5C）：当内在速度大于目标运动速度时，预测就发生了。

CANN的这种强大预测跟踪能力也为我们提供了一种类脑的运动目标跟踪算法。该算法的优点包括：

预测跟踪的时间是恒定的，几乎不依赖于目标运动速度；
模型的参数是可以根据任务，理论上预先设定的，不需要网络训练；
CANN及反馈机制可以被类脑芯片实现。

在这里对CANN with Adaptation模型简要地阐述： $$ \begin{align*} \
&\tau \, \frac{du(x, t)}{dt} = -u(x,t) + \rho \int dx' J(x,x')\, r(x',t) - V(x,t) + I_{ext} \\
\\
&\tau_v \, \frac{dV(x,t)}{dt} = - V(x,t) + m\,U(x,t)\
\
\end{align*} $$

3、多模态信息整合

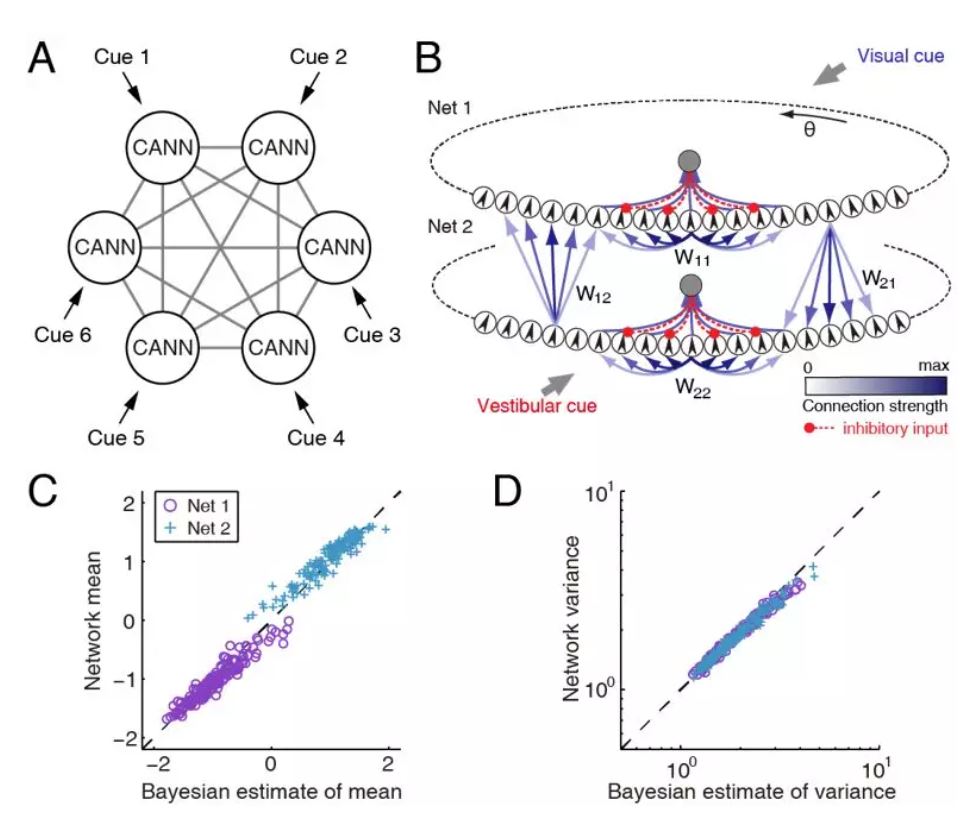
从计算的角度看，在整合这些不同属性或特征的信号时，大脑需要一种共同的信息表达模式，才能相互交流信息。CANN，在其中信息被统一表达为神经群活动波包，为多模态信息整合提供了一种可能的操作平台。我们研究了视觉和平衡觉信息整合来感知头朝向(heading direction)的神经网络模型。依据实验数据，我们提出了去中心化的计算模型，其中MSTd上的CANN主要接受视觉信号，而VIP上的CANN主要接受平衡觉信号，两者之间通过长程连接交换信息（图6）。我们的研究表明两个耦合的CANN能够可以实现贝叶斯优化信息整合，也可以实现统计优化的信息分离，初步支持了CANN可以作为大脑内信息表达、储存、运算、和交流的统一网络框架。

图6：CANN实现优化的多模态信息整合。A，去中心化的信息整合网络结构示意图。B，两个耦合的CANN，分别接受视觉和平衡觉信号，共同计算自身运动的方向。C和D，网络计算结果和统计优化的贝叶斯理论符合。

总结

在讲座中老师还提到了很多前景和应用，在这里我简单罗列一下：

Levy Flight in CANN: Levy FLight是一种运动模式，可以与布朗运动类比，其特点是一段小范围的随机游走后会进行一次距离较大的转移，这种特性和大脑联想记忆机制很相似。而CANN在tracking上根据内在速度和目标速度的三种关系（小于、等于、大于）分成了三种tracking模式，其中一种Oscillation tracking模式，这种模式和联合记忆机制有着很大的关联，这一话题会在后续和老师交流以后单独写一个博客讲解。
Phase pre- and pro-cession with CANN: to be continue

CANN代码

source: BrainModel from PKU-NIP-LAB

import numpy as np
import brainpy as bp


class CANN1D(bp.NeuGroup):
    target_backend = ['numpy', 'numba']

    @staticmethod
    def derivative(u, t, conn, k, tau, Iext):
        r1 = np.square(u)
        r2 = 1.0 + k * np.sum(r1)
        r = r1 / r2
        Irec = np.dot(conn, r)
        du = (-u + Irec + Iext) / tau
        return du

    def __init__(self, num, tau=1., k=8.1, a=0.5, A=10., J0=4.,
                 z_min=-np.pi, z_max=np.pi, **kwargs):
        # parameters
        self.tau = tau  # The synaptic time constant
        self.k = k  # Degree of the rescaled inhibition
        self.a = a  # Half-width of the range of excitatory connections
        self.A = A  # Magnitude of the external input
        self.J0 = J0  # maximum connection value

        # feature space
        self.z_min = z_min
        self.z_max = z_max
        self.z_range = z_max - z_min
        self.x = np.linspace(z_min, z_max, num)  # The encoded feature values

        # variables
        self.u = np.zeros(num)
        self.input = np.zeros(num)

        # The connection matrix
        self.conn_mat = self.make_conn(self.x)

        self.int_u = bp.odeint(f=self.derivative, method='rk4', dt=0.05)

        super(CANN1D, self).__init__(size=num, **kwargs)

        self.rho = num / self.z_range  # The neural density
        self.dx = self.z_range / num  # The stimulus density

    def dist(self, d):
        d = np.remainder(d, self.z_range)
        d = np.where(d > 0.5 * self.z_range, d - self.z_range, d)
        return d

    def make_conn(self, x):
        assert np.ndim(x) == 1
        x_left = np.reshape(x, (-1, 1))
        x_right = np.repeat(x.reshape((1, -1)), len(x), axis=0)
        d = self.dist(x_left - x_right)
        Jxx = self.J0 * np.exp(-0.5 * np.square(d / self.a)) / (np.sqrt(2 * np.pi) * self.a)
        return Jxx

    def get_stimulus_by_pos(self, pos):
        return self.A * np.exp(-0.25 * np.square(self.dist(self.x - pos) / self.a))

    def update(self, _t):
        self.u = self.int_u(self.u, _t, self.conn_mat, self.k, self.tau, self.input)
        self.input[:] = 0.

# population encoding
cann = CANN1D(num=512, k=0.1, monitors=['u'])

I1 = cann.get_stimulus_by_pos(0.)
Iext, duration = bp.inputs.constant_current([(0., 1.), (I1, 8.), (0., 8.)])
cann.run(duration=duration, inputs=('input', Iext))

bp.visualize.animate_1D(
    dynamical_vars=[{'ys': cann.mon.u, 'xs': cann.x, 'legend': 'u'},
                    {'ys': Iext, 'xs': cann.x, 'legend': 'Iext'}],
    frame_step=1,
    frame_delay=100,
    show=True,
    # save_path='../../images/CANN-encoding.gif'
)

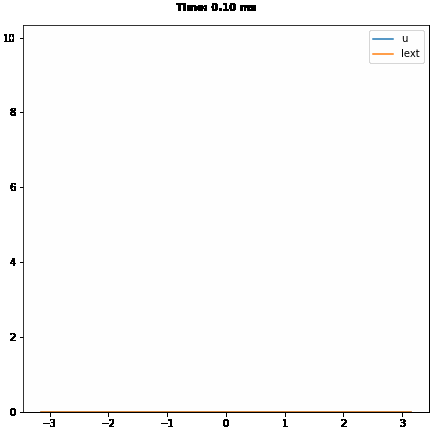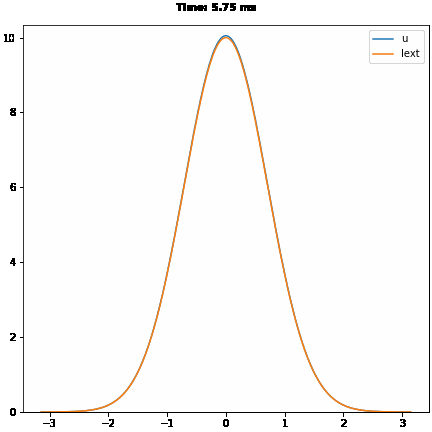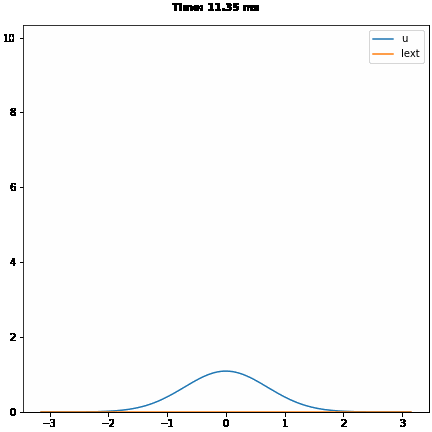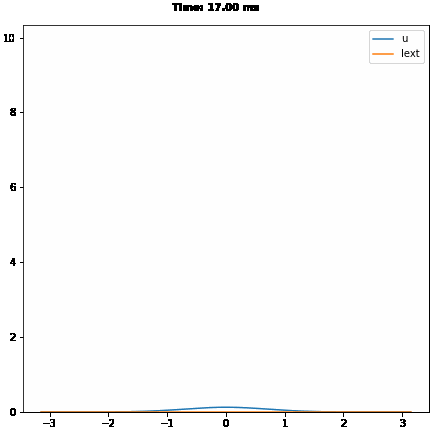
# template matching

cann = CANN1D(num=512, k=8.1, monitors=['u'])

dur1, dur2, dur3 = 10., 30., 0.
num1 = int(dur1 / bp.ops.get_dt())
num2 = int(dur2 / bp.ops.get_dt())
num3 = int(dur3 / bp.ops.get_dt())
Iext = np.zeros((num1 + num2 + num3,) + cann.size)
Iext[:num1] = cann.get_stimulus_by_pos(0.5)
Iext[num1:num1 + num2] = cann.get_stimulus_by_pos(0.)
Iext[num1:num1 + num2] += 0.1 * cann.A * np.random.randn(num2, *cann.size)
cann.run(duration=dur1 + dur2 + dur3, inputs=('input', Iext))

bp.visualize.animate_1D(
    dynamical_vars=[{'ys': cann.mon.u, 'xs': cann.x, 'legend': 'u'},
                    {'ys': Iext, 'xs': cann.x, 'legend': 'Iext'}],
    frame_step=5,
    frame_delay=50,
    show=True,
    # save_path='../../images/CANN-decoding.gif'
)

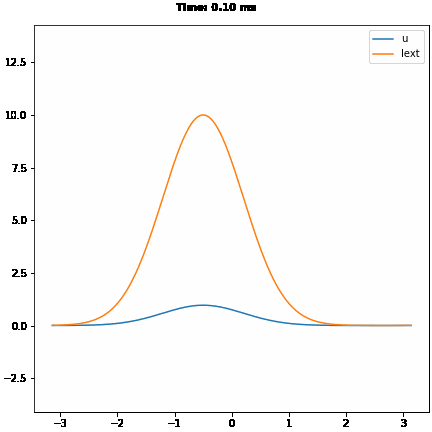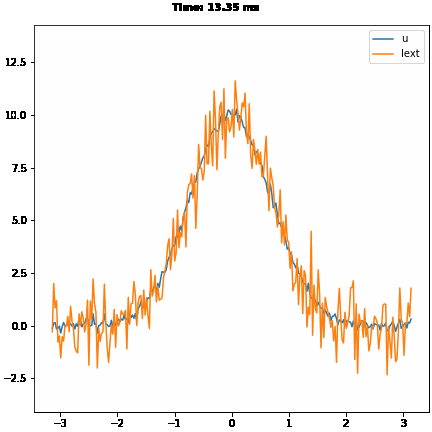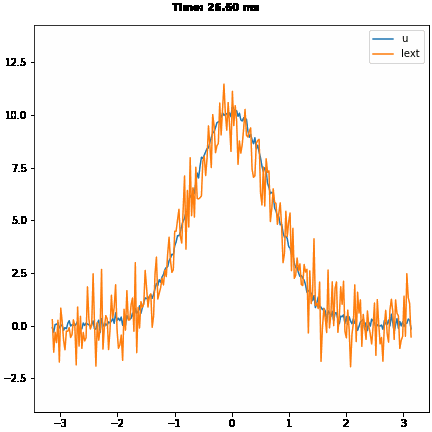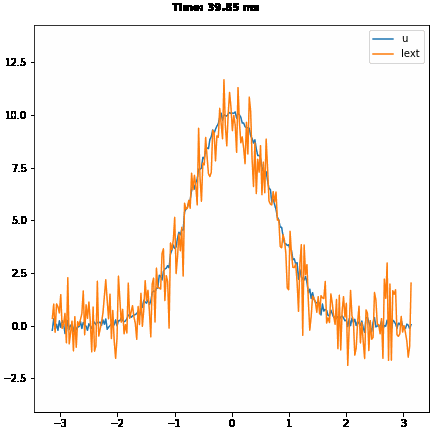
# smooth tracking

cann = CANN1D(num=512, k=8.1, monitors=['u'])

dur1, dur2, dur3 = 20., 20., 20.
num1 = int(dur1 / bp.ops.get_dt())
num2 = int(dur2 / bp.ops.get_dt())
num3 = int(dur3 / bp.ops.get_dt())
position = np.zeros(num1 + num2 + num3)
position[num1: num1 + num2] = np.linspace(0., 12., num2)
position[num1 + num2:] = 12.
position = position.reshape((-1, 1))
Iext = cann.get_stimulus_by_pos(position)
cann.run(duration=dur1 + dur2 + dur3, inputs=('input', Iext))

bp.visualize.animate_1D(
    dynamical_vars=[{'ys': cann.mon.u, 'xs': cann.x, 'legend': 'u'},
                    {'ys': Iext, 'xs': cann.x, 'legend': 'Iext'}],
    frame_step=5,
    frame_delay=50,
    show=True,
    # save_path='../../images/CANN-tracking.gif'
)

Brandon Zhang