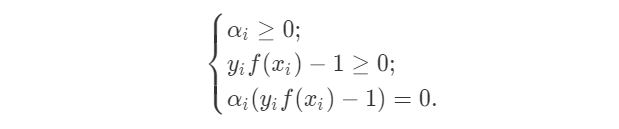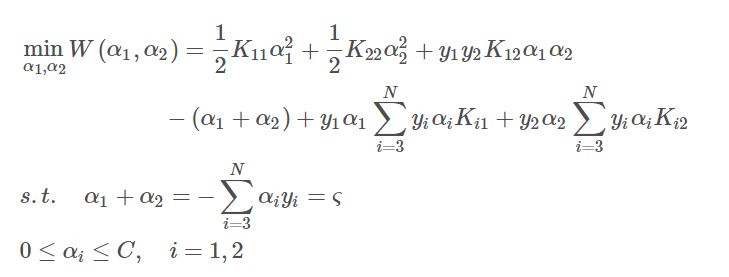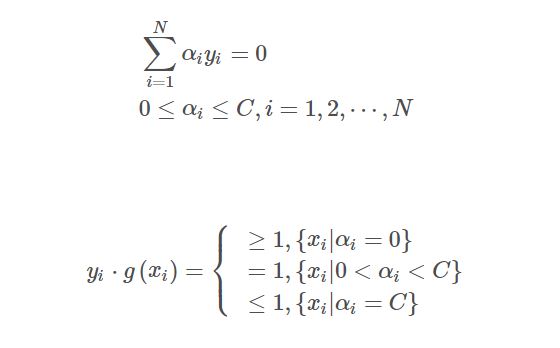Support Vector Machines
支持向量机模型
- 学习策略:间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的最优化问题
一、线性可分支持向量机与硬间隔最大化
支持向量机的学习是在特征空间上进行的,需要从输入空间转换到特征空间上。
线性可分支持向量机:给定线性可分的训练集,通过间隔最大化或等价地求解相应的凸二次规划问题得到的分离超平面为: $$\omega^* x + b^* = 0$$ 以及相应的分类决策函数: $$f(x) = sign(\omega^* x + b^*)$$
函数间隔和几何间隔
- 函数间隔:对于给定的训练数据集$T$和超平面$(\omega, b)$,则
$$\hat{\gamma_i}=y_i(\omega \cdot x_i+b)$$
超平面关于数据集$T$的函数间隔为 $$\hat{\gamma}=\min_{i=1,\dots,N}\hat{\gamma_i}$$ - 几何间隔:对于给定的训练数据集$T$和超平面$(\omega, b)$,则
$$\hat{\gamma_i}=y_i(\frac{\omega}{||\omega||} \cdot x_i+\frac{b}{||\omega||})$$
其中$||\omega||$是L2范数。
- 函数间隔:对于给定的训练数据集$T$和超平面$(\omega, b)$,则
$$\hat{\gamma_i}=y_i(\omega \cdot x_i+b)$$
间隔最大化
- 输入:线性可分数据集$T$
- 输出:最大间隔分离超平面和分类决策函数
- 构造并求解约束最优化问题: $$\min_{\omega,b} \quad \frac{1}{2}||\omega||^2 $$ $$ s.t. \qquad y_i(\omega \cdot x_i+b)-1 \geq 0, \quad i=1, 2, \dots, N$$
- 求解得到最优解$\omega^* , b^*$。
支持向量
- 训练集的样本点中与分离超平面距离最近的样本点的实例: $$H_1:\omega \cdot x_i+b=1 $$ $$H_2:\omega \cdot x_i+b=-1$$
支持向量机由这些很少的“重要”训练样本决定。
求解方法:应用拉格朗日对偶法,通过求解对偶问题得到原始问题的最优解。
- 输入:线性可分训练集$T$;
- 输出:分离超平面和分类决策函数
- 构造并求解约束最优化问题: $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j)-\sum_{i=1}^{N}\alpha_i $$ $$ s.t. \qquad \sum_{i=1}^{N} \alpha_iy_i=0 $$ $$ \alpha_i \geq 0, i = 1,2,\dots,N $$ 并求出最优解$\alpha^*$。
- 计算 $$\omega^* = \sum_{i=1}^N\alpha_i^*y_ix_i$$ 并选择$\alpha^*$的其中一个正分量$\alpha^*\gt 0$,计算 $$b^*=y_i- \sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)$$
- 求得分离超平面 $$\omega^* \cdot x+ b^* =0$$
- 分类决策函数: $$f(x)=sign(\omega^* \cdot x+b^* )$$
二、线性支持向量机与软间隔最大化
线性支持向量机:给定线性不可分的训练集,通过软间隔最大化或等价地求解相应的凸二次规划问题得到的分离超平面为: $$\omega^* x + b^* = 0$$ 以及相应的分类决策函数: $$f(x) = sign(\omega^* x + b^*)$$
软间隔最大化 输入:线性可分数据集$T$ 输出:最大间隔分离超平面和分类决策函数 构造并求解约束最优化问题: $$\min_{\omega,b} \quad \frac{1}{2}||\omega||^2 + C\sum_{i=1}^N\xi_i$$ $$ s.t. \qquad y_i(\omega \cdot x_i+b)\geq 1-\xi_i, \quad i=1, 2, \dots, N$$ $$ \xi_i \ge 0,\quad i=1, 2, \dots, N $$ 求解得到最优解$\omega^*, b^*$。
求解方法
- 输入:线性可分训练集$T$;
- 输出:分离超平面和分类决策函数
- 构造并求解约束最优化问题: $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j)-\sum_{i=1}^{N}\alpha_i $$ $$ s.t. \qquad \sum_{i=1}^{N} \alpha_iy_i=0 $$ $$ 0 \leq \alpha_i \leq C, i = 1,2,\dots,N $$ 并求出最优解$\alpha^*$。
- 计算 $$\omega^* = \sum_{i=1}^N\alpha_i^*y_ix_i$$ 并选择$\alpha^*$的一个适合条件$0\lt\alpha^*\lt C$,计算 $$b^*=y_i- \sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)$$
- 求得分离超平面 $$\omega^* \cdot x+b^* =0$$
- 分类决策函数: $$f(x)=sign(\omega^* \cdot x+b^*)$$
上述过程需要满足KKT(Karush-Kuhn-Tucker)条件,即:
对于任意样本$(x_i, y_i)$,总有$\alpha_i=0$ 或 $y_if(x_i)-1=0$。当$\alpha_i \gt 0$时,则必有$y_if(x_i)=1$,则所有的样本点位于最大间隔边界,是一个支持向量。所以最终模型只和支持向量有关。
合并损失函数(linge loss function) 线性支持向量机的另一种最优化问题是,最小化以下函数: $$\sum_{i=1}^{N}[1-y_i(\omega \cdot x_i + b)]_++\lambda||\omega||^2$$
其中第一项为合页损失函数。
三、非线性支持向量机与核函数
核技巧
基本想法:通过一个非线性变换将输入空间(欧式空间$\mathcal{R}^n$或离散集合)对应于一个特征空间(希尔伯特空间$\mathcal{H}$),使得在输入空间$\mathcal{R}^n$中的超曲面模型对应特征空间$\mathcal{H}$中的超平面模型。
- 核函数的定义:
- 核函数的定义:
在支持向量机中的应用:
在核函数$K(x,z)$给定的条件下,可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。在实际应用中,往往依赖领域知识直接选择核函数,核函数选择的有效性需要通过实验验证。
正定核
这部分需要泛函分析的知识,目前来看可能需要研究生再看懂了。 对称函数$K(x,z)$为正定核的充要条件如下: 对任意$x_i \in \mathcal{X}, i=1,2,\dots,m$,任意正整数$m$,对称函数$K(x,z)$对应的Gram矩阵是半正定的。
常用核函数
- 多项式核函数(polynomial kernel function) $$K(x,z)=(x\cdot z+1)^p$$
- 高斯核函数(Gaussian kernel function) $$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})$$
- 字符串核函数(string kernel function) 用于文本分类、信息检索、生物信息学等方面。直观上,两个字符串相同的子串越多,它们就越相似、字符串核函数的值就越大。
求解方法
- 输入:训练集$T$;
- 输出:分离超平面和分类决策函数
- 构造并求解约束最优化问题: $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i \cdot x_j)-\sum_{i=1}^{N}\alpha_i $$ $$ s.t. \qquad \sum_{i=1}^{N} \alpha_iy_i=0 $$ $$ 0 \leq \alpha_i \leq C, i = 1,2,\dots,N $$ 并求出最优解$\alpha^*$。
- 计算 $$\omega^* = \sum_{i=1}^N\alpha_i^*y_ix_i$$ 并选择$\alpha^*$的一个适合条件$0\lt\alpha^*\lt C$,计算 $$b^*=y_i- \sum_{i=1}^N\alpha_i^*y_iK(x_i\cdot x_j)$$
- 求得分离超平面 $$\omega^* \cdot x+b^*=0$$
- 分类决策函数: $$f(x)=sign\left( \sum_{i=1}^N\alpha_i^* y_iK(x\cdot x_i+b^*)\right)$$
四、序列最小最优算法SMO
算法描述如下:
输入:训练集$T$
输出:近似解$\hat{\alpha}$
取初值$\alpha^{(0)}=0$,令$k=0$。
选取优化变量$\alpha_1^{(k)}, \alpha_2^{(k)}$,解析求解两个变量的最优化问题:
求得最优解$\alpha_1^{(k+1)}, \alpha_2^{(k+1)}$,更新$\alpha$为$\alpha^{(k+1)}$。
- 若在精度$\epsilon$范围内满足停机条件:
其中, $$g(x_i)=\sum_{j-1}^N\alpha_jy_jK(x_j,x_i)+b$$ 则转(4);否则令$k=k+1$,转(2);
- 取$\hat{\alpha}=\alpha^{(k+1)}$。