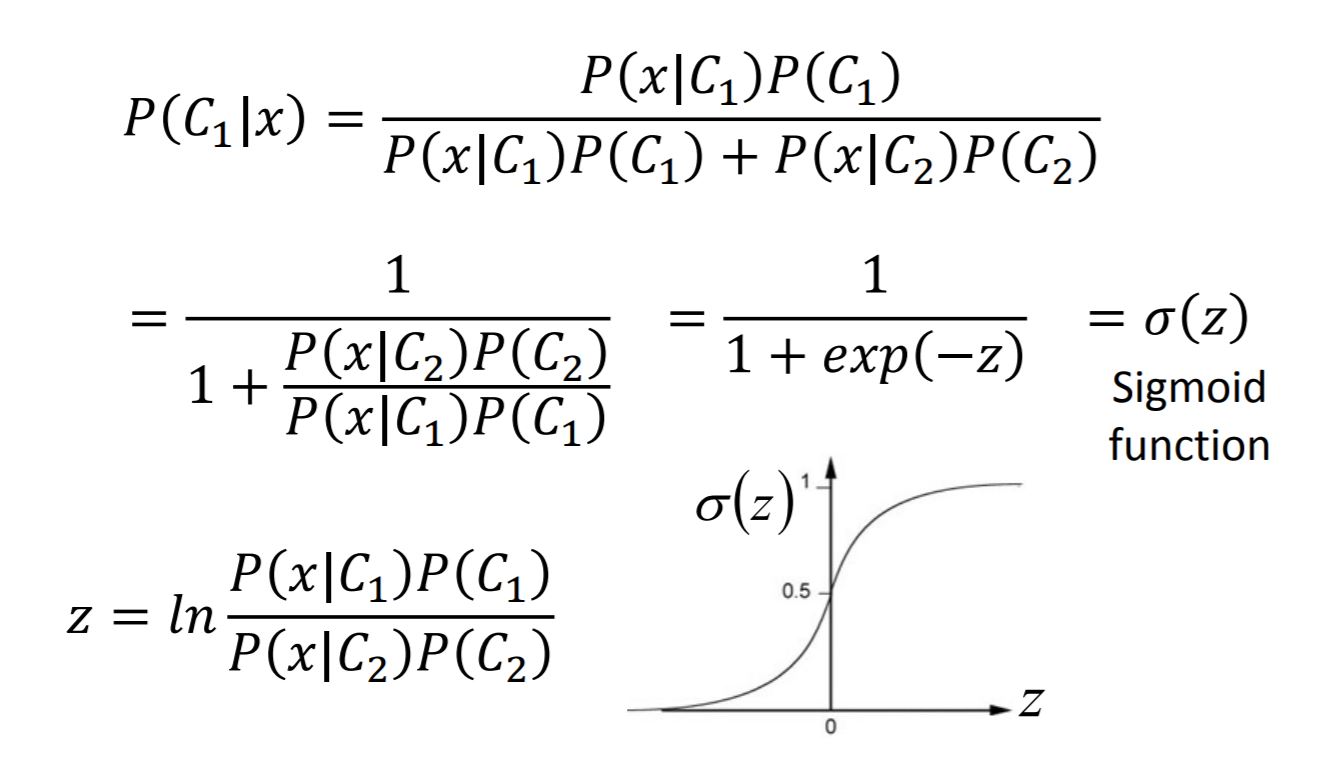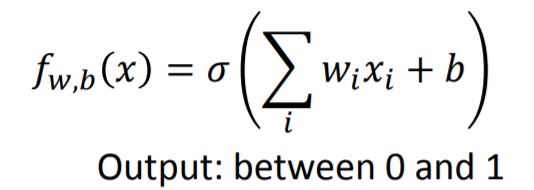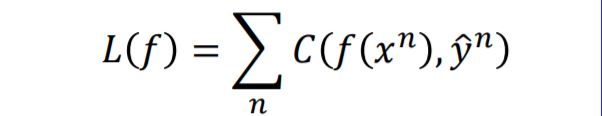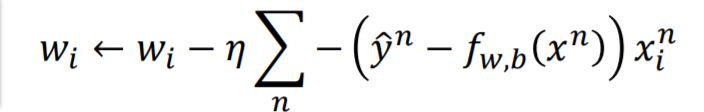Classification

I. Probabilistic Generative Models

1. Detailed Process

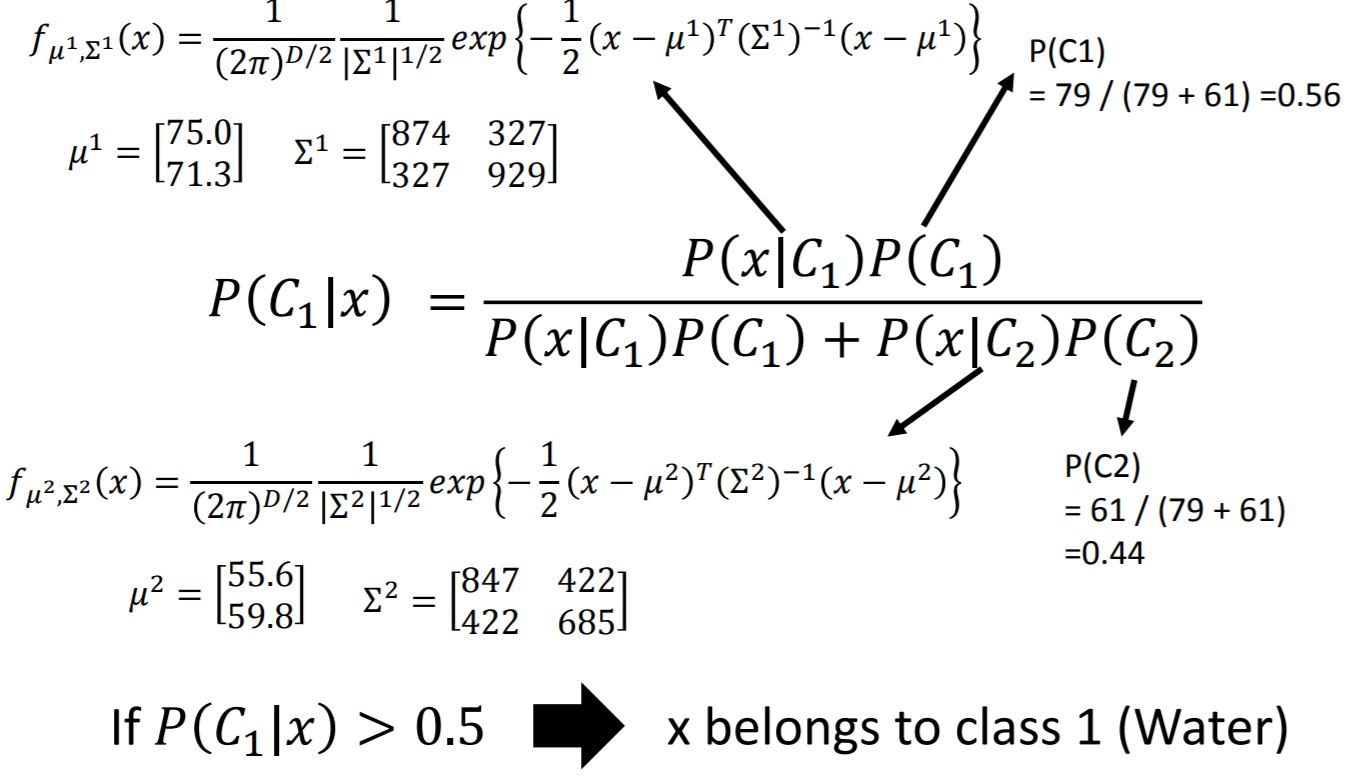
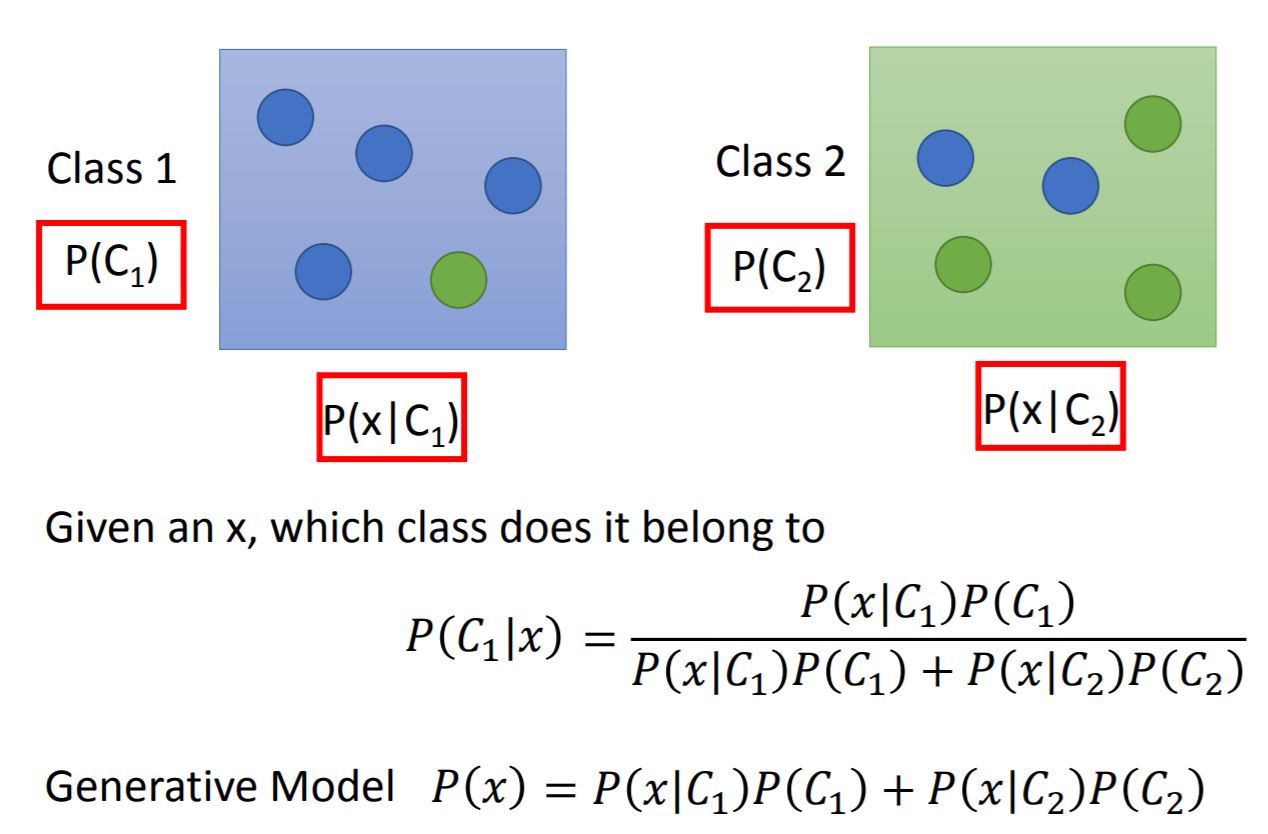
The basic idea is estimating the probabilities form training data. Let’s consider the two classes case: First of all, we need to figure out prior class probabilities $P(C_k)$. It’s pretty easy to find that $P(C_k) = \frac{SizeOf C_k}{SizeOf Training Data}$ Then the task is to find out $P(x|C_k)$. Each data is represented as a vector by its attribute, and it exist as a point in a multidimensional space. We assume the points are sampled from a Gaussian distribution. Once we have specified a parametric functional form for the class-conditional densities $P(x|C_k)$, we can then determine the values of the parameters, together with the prior class probabilities $P(C_k)$, using maximum likelihood. This requires a data set comprising observations of x along with their corresponding class labels. The parameters of Gaussian Distribution are mean $\mu$ and covariance matrix $\Sigma$. The Gaussian with any mean $\mu$ and covariance matrix $\Sigma$ can generate these points. In this example, we assume $x^1, x^2, \dots, x^{79}$ generate from the Gaussian ($\mu^{}$, $\Sigma^{}$) with the maximum likelihood. Now we come back to the formula given before, all the value of probabilities are figured out and we could substitute in to get this result.

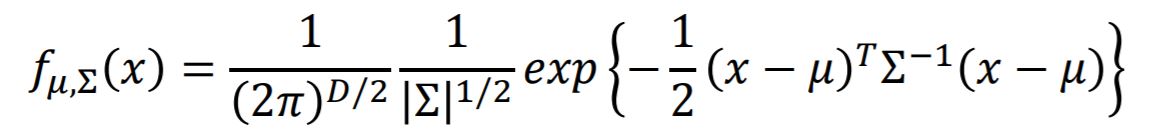
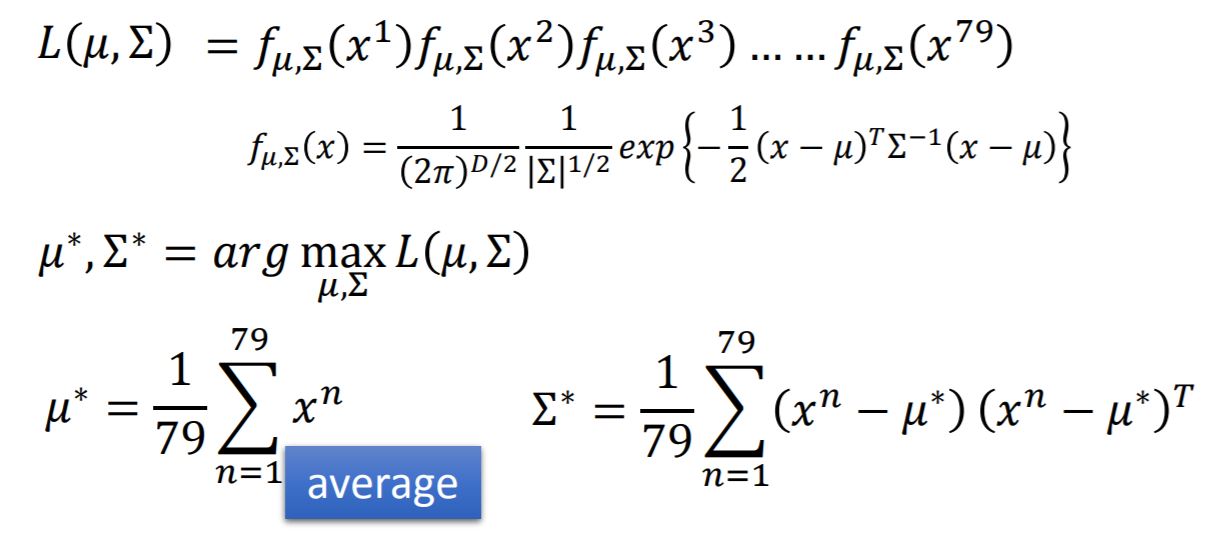
2. Modifying Model

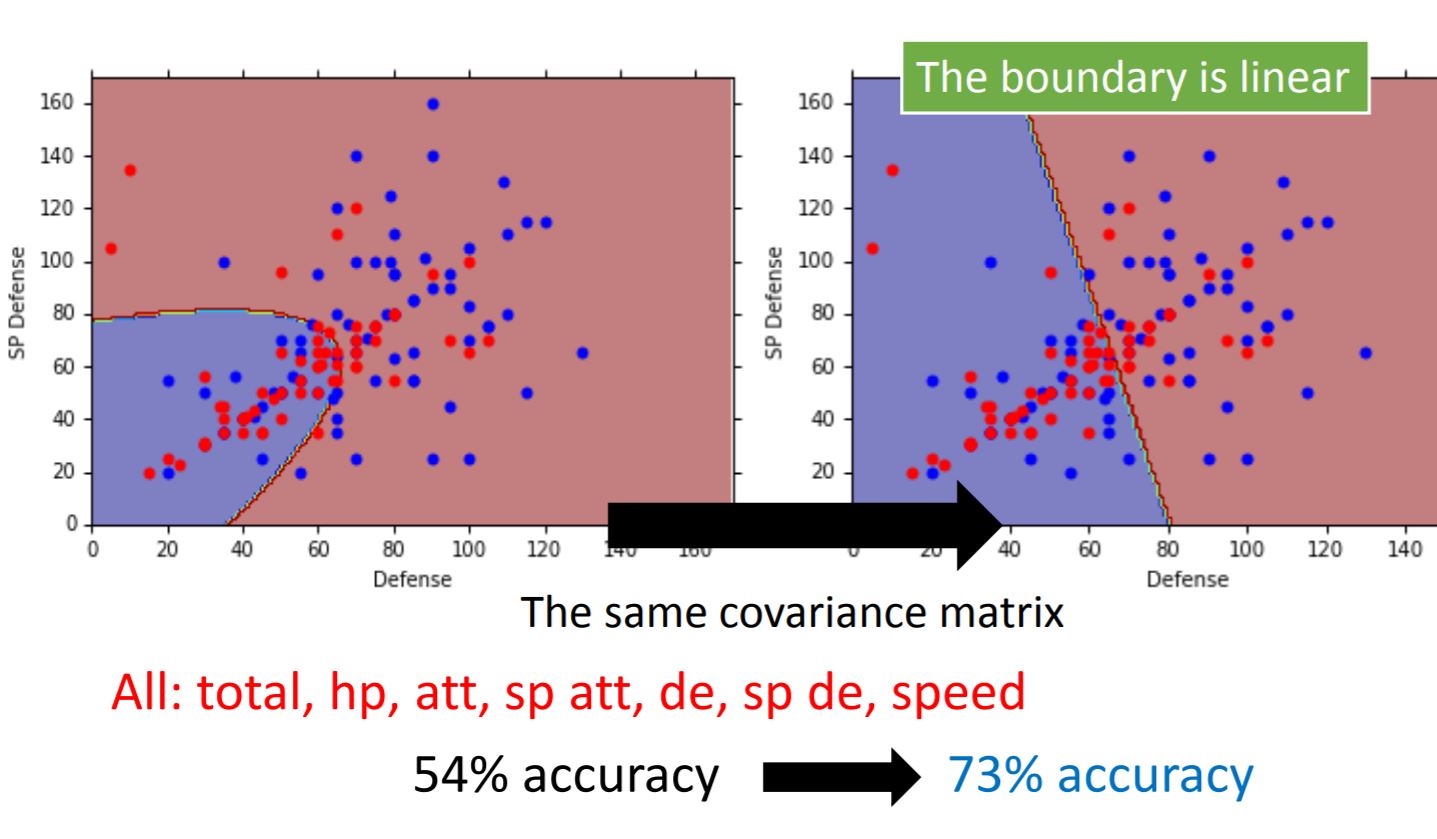
While we are training the model, we normally choose the same covariance matrix $\Sigma$ for each Gaussian Distribution. The reason for doing this is to have less parameters for the training model, also from the result we can see the accuracy has increased (Maybe just in this case).

3. Summary

4. Tips

  • Posterior Probability & Sigmoid function
  • Posterior Probability & Logistic Regression

II. Logistic Regression

1. Detailed Process

Step 1: Function Set

Step 2: Goodness of Function

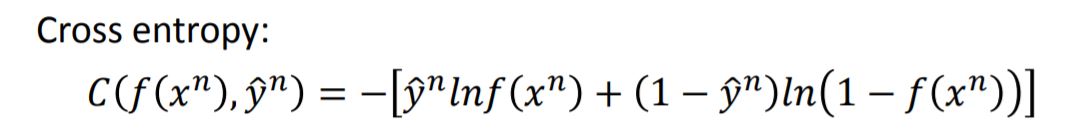
Cross entropy (交叉熵) : 如果两个分布相同，则交叉熵为0。In logistic regression we have training data $(x^n, \hat{y}^n)$, where $\hat{y}^n$: 1 for class 1, 0 for class 2. Then we have the loss function as below:

Step 3: Gradient Descent

The update function of parameter $\omega$ is:

2. Discriminative vs Generative

  • The benefits of Generative model
    • With the assumption of probability distribution, less training data is needed;
    • With the assumption of probability distribution, more robust to the noise;
    • Priors and class-dependent probabilities can be estimated from different sources.

      关于第三点需要着重解释一下。对于大部分神经网络都是判别模型，这种模型也确实会有更高的准确率。但对于类似语音识别的task中，priors和class-dependent probabilities是可以分开计算的，例如先验概率是由海量的网上数据计算而得，而class-dependent probabilities是根据语音数据计算得来。

3. Multi-class Classification

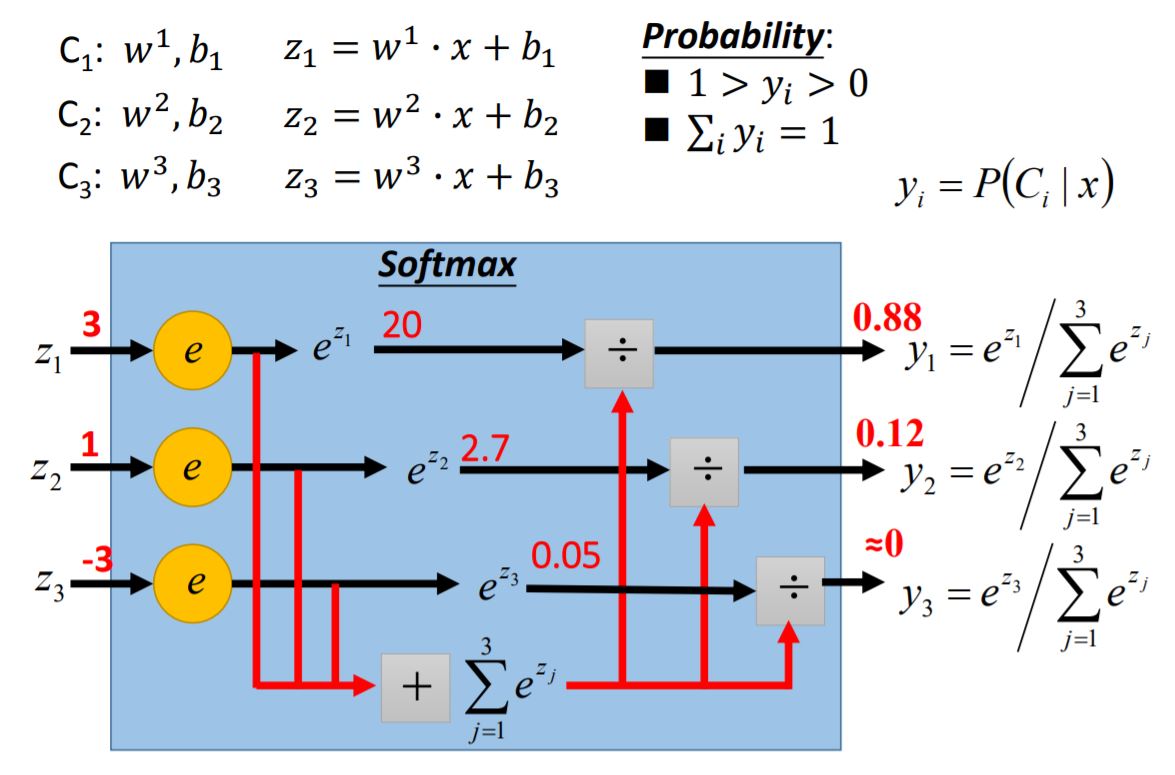
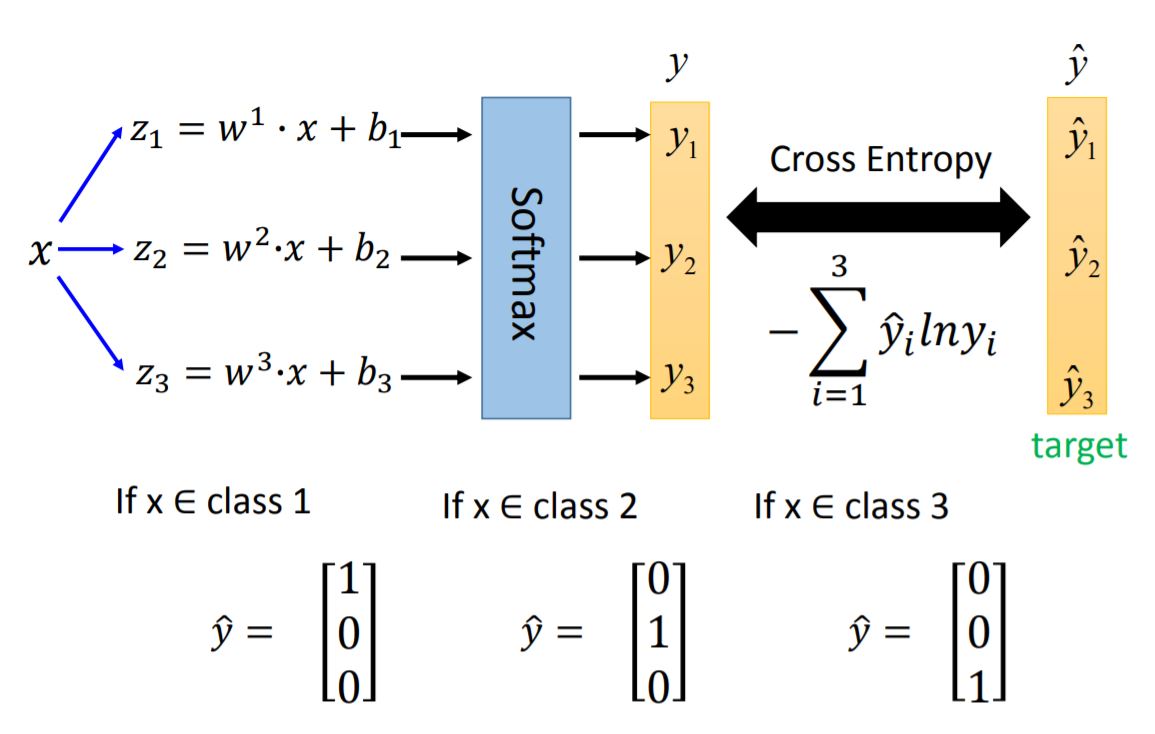
这种对 $\hat{y}$ 的编码方式称为独热编码 (One-Hot Encoding)

4. Limitation of Logistic Regression

  • XOR Problem can’t be solved by Logistic Regression.

  • Solution

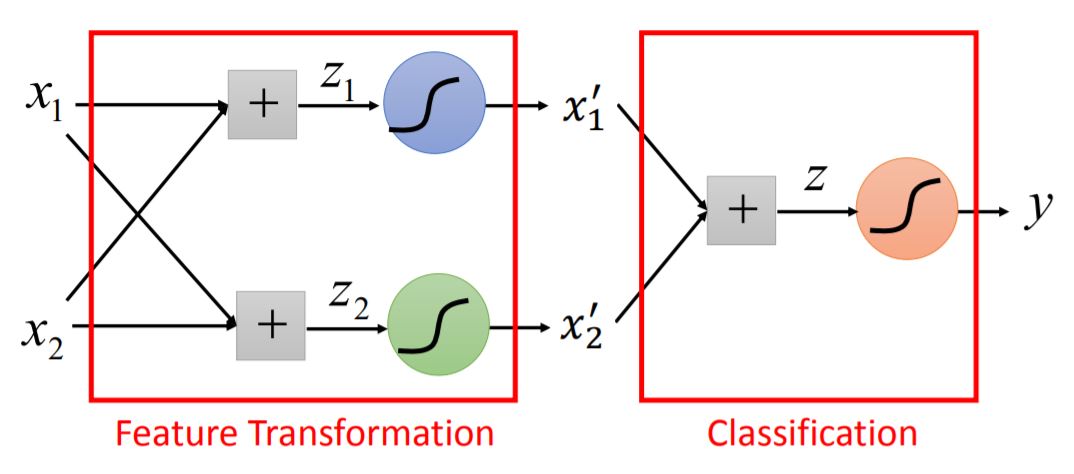
    1. Feature Transformation It’s not always easy to find a good transformation. (与SVM中的Kernel函数类似)

    2. Cascading logistic regression models 中间的变换为分线性变换，使得在后续可分。