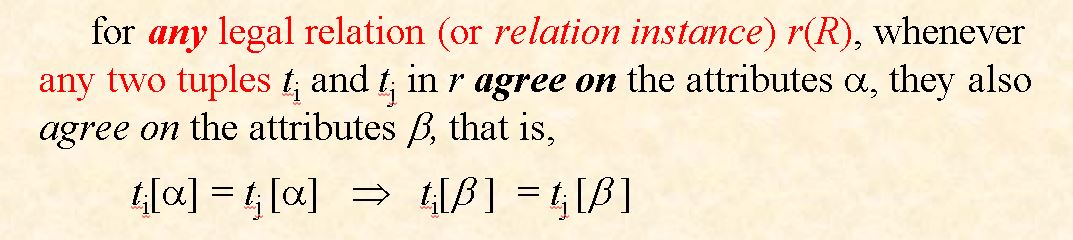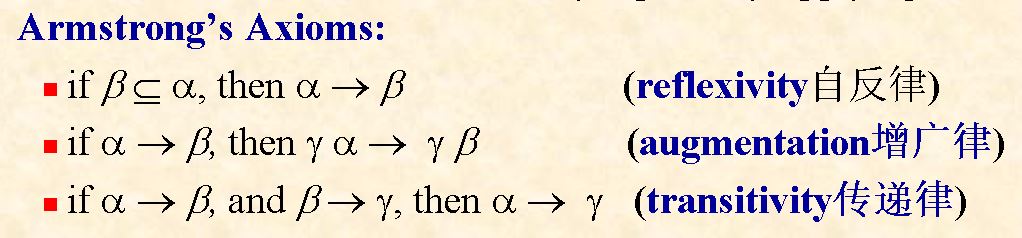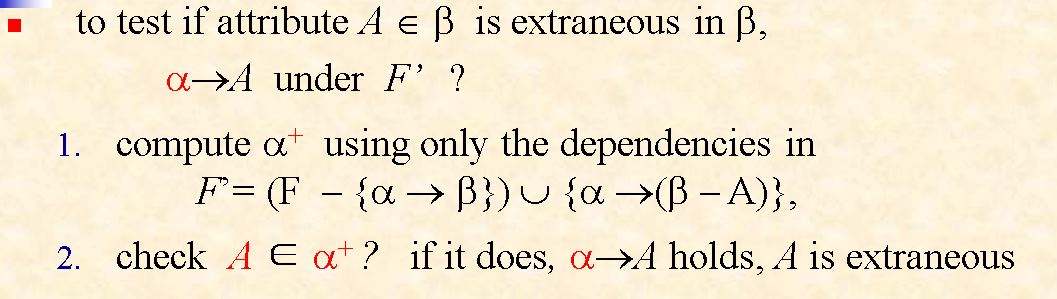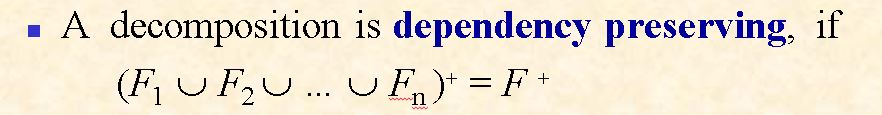Chapter 7 Database Design and E-R Model

7.2 Concepts

  1. Entity sets
  2. Relationship sets 对于多元联系$\Rightarrow$二元联系$\Rightarrow$关系表
  3. Attribute

7.3 Constraints

  1. Mapping Cardinalities
    • one to one
    • one to many
    • many to one
    • many to many
  2. Keys
    • superkey
    • candidate key
    • primary key

Chapter 8 Schema Normalization

核心思想：将large schemas decompose to smaller schema. 建立functional dependency, 并利用两表查询的的方式进行查询(此处详见第7章)。 在第7章通过将E-R图进行转换，得到面向特定的初始关系模式集，这些关系模式集可能存在多种数据依赖关系：

  • Functional Dependencies
  • Multivalued Dependencies
  • Join Dependencies (略)

如果直接根据初始关系模式构造DBS，由于初始关系模式中数据依赖关系的存在，可能会违反DB的完整性约束

  • pitfalls：插入、更新、删除问题

因此，对初始关系模式集，需要根据关系规范化理论，在保证关系模式的

  • lossless join
  • dependency preservation

步骤大致为：

  • 根据函数依赖的Armstrong’s 公理系统 ( §8.4.1 )和多值依赖 的公理系统 ，从初始关系模式集中已知的函数依赖和多值依赖出发，推导出初始关系模式集中所有的函数依赖（§8.4)和多值依赖(不作要求)
  • 模式分解算法，对其进行（等价）分解和变换，将其转换为各种范式形式。

8.2 Atomic Domains and First Normal Form

  1. Atomic Domains: its elements are considered to be indivisible units. 反例：集合(非原子域)、复合属性等

  2. First Normal Form: A relational schema R is in first normal form if the domains of all attributes of R are atomic

8.3 Decomposition Using Functional Dependencies

8.3.1 Functional Dependencies

  1. Def1: Functional dependency(FD) holds on R

  2. Keys in relational schema can be defined in terms of FD

    • K is a superkey for relation schema R, if and only if $k \rightarrow R$
    • K is a candidate key for R, if and only if
      • $k \rightarrow R$,
      • and for no $\alpha \subset K, \alpha \rightarrow R$

  3. Def2: (A particular relation instance) r(R) satisfy FD, or FD is satisfied by r(R).

How to guarantee the FD in DBS? answer：用SQL检查2个属性之间的FD

  1. FD holds on R: 整体要求，定义在R的属性间的语义约束 FD is satisfied by r(R): 部分满足 意思是对于关系R而言，即使它的关系实例r(R)满足某些FD，也不能代表整个关系R就满足该FD！可能只是该关系实例的数据凑巧满足而已。(容易出判断题考察)

  2. Trivial FD: 所有关系实例均满足FD，大多是右边属性包含于左边

  3. Transitive dependency (传递函数依赖)

  4. Partial dependency (部分函数依赖) 即对于$\alpha \rightarrow \beta$中，$\alpha$含有冗余项。

  5. Closure of FD The set of all functional dependencies logically implied by F is the closure of F, denoted as $F^+$.

8.3.2 Boyce-Codd Normal Form

  1. Def: 每一个FD需要满足其中之一的性质
  2. Decomposing a Schema into BCNF: 相当于外键关联

ATTENTION：BCNF 并不能保持函数依赖，所以需要考虑上一级的3NF

8.3.4 Third Normal Form

  1. Def:在BCNF的定义中添加该性质

  2. 性质：(必要条件)

    • R is also in 2NF
    • 不存在非主属性对候选键的部分和传递依赖，i.e.每一个非主属性都不传递依赖于R的任何候选键

重要！！！！ 检测关系模式是否满足函数依赖的方法

8.4 Functional-Dependency Theory

8.4.1 Closure of a Set of FD

定义在上面已经给出

  1. Logically implied: Given a schema R, a functional dependency f on R is logically implied by a set of FD F on R , if every instance r(R) that satisfies F also satisfies f. 简而言之，某个函数依赖f可以被F这个集合推出来

  2. Armstrong’s Axioms

8.4.2 Closure of Attribute Sets

  1. Def: An attribute B is functionally determined by $\alpha$ if $\alpha \rightarrow B$.

  2. Def 注意该集合是有限的

  3. 若通过某些属性推出R，说明其为superkey，接下来判断其是否是candidate key.

  4. Uses of Attribute Closure 这里的第二种用途是第二种测试函数依赖的方法，相比SQL方法更为简单方便。

  5. 等价的概念

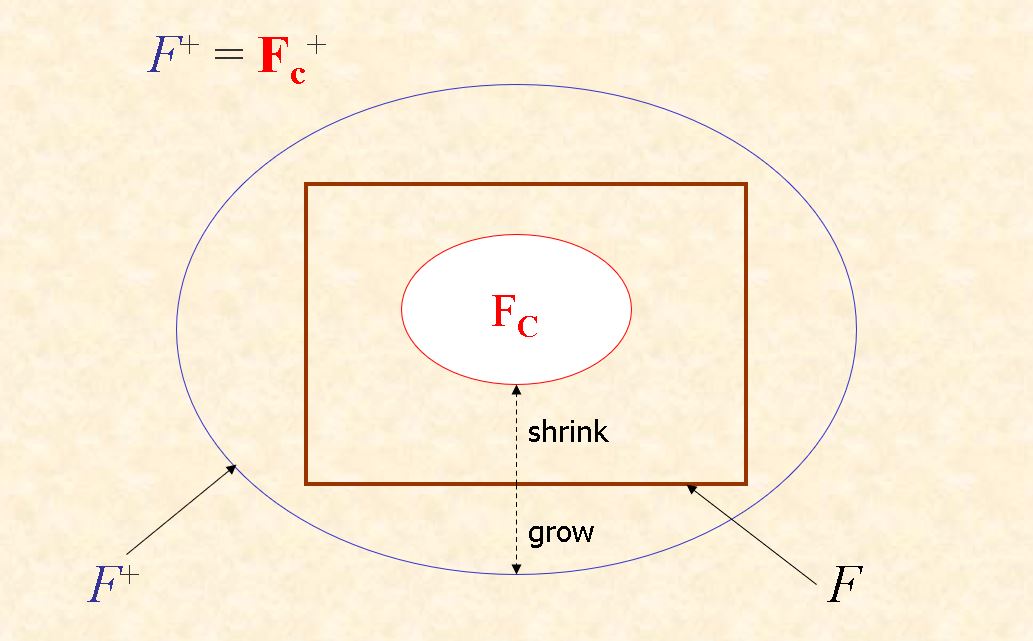
8.4.3 Canonical Cover

用于去除FD set中函数依赖的左右两端的冗余项。正则覆盖是最小的与F等价的函数依赖集合，记作$F^+ = F^+_c$。

  1. Extraneous Attributes

  2. 两种情况的解决问题方案

    • 当冗余元素在左边出现的时候 在原有函数依赖下，求属性闭包，用于判断冗余属性
    • 当冗余元素在右边出现的时候 在新的函数依赖之下求属性闭包

  3. A canonical cover for F is a set of dependencies Fc such that 所有函数依赖的左边不会相同，这种判断方法来源于求出canonical cover的算法。

  4. Compute a canonical cover

8.4.4 Lossless-join Decomposition

不同子表间存在外键关联。 该定理意思是对于两个关系表，他们的公共属性可以推出至少其中一张关系表的所有属性，则根据公共元素分解后的分解方式为无损分解。

8.4.5 Dependency Preserving

  1. Restriction of F to Ri

  2. Dependency Preserving 子模式FD成立可以推出原模式FD成立，用于测试dependency preserving。

注意以下这种情况： 看似$A\rightarrow D$并不能满足，但有以下关系： $A|F_1 \rightarrow B, B|F_2 \rightarrow D$, so $A\rightarrow D$ is preserved.

$A|F_1$ 代表在函数依赖集$F_1$下A可以推出的attributes sets

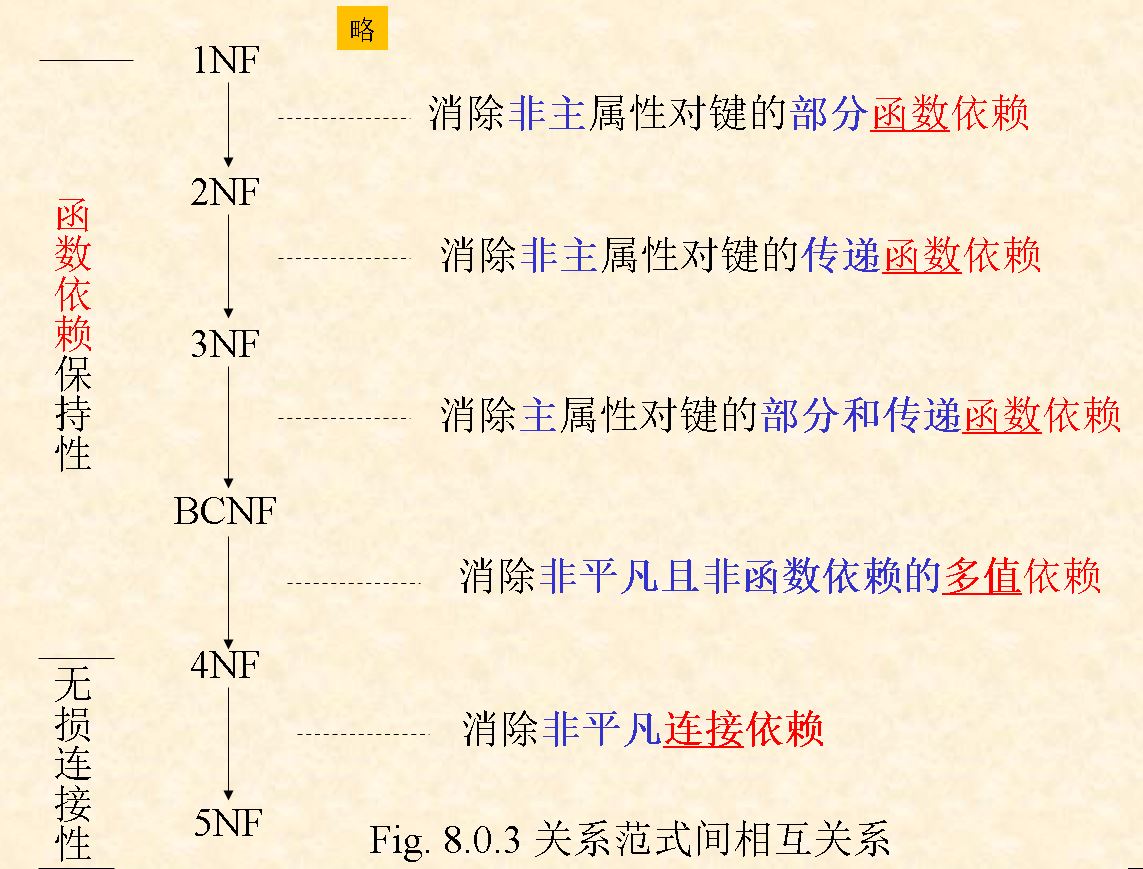
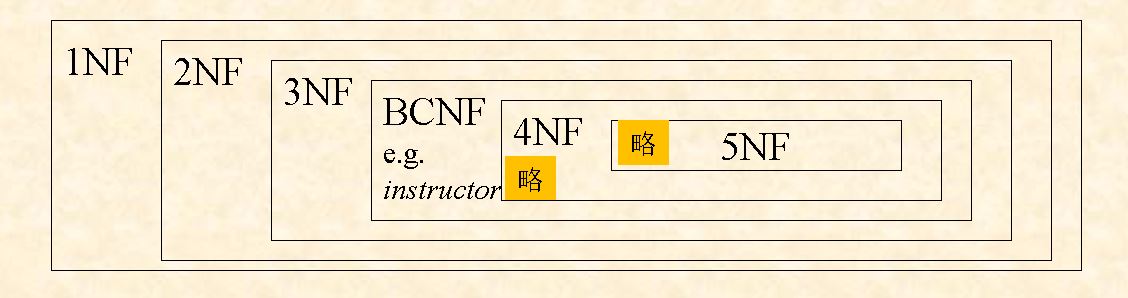
总结：范式之间的关系

  1. Second Normal Form 相当于第二范式的每一个函数依赖的左边不能出现可分的超键。

  2. Third Noramal Form

  3. BCNF

8.5 Algorithms for Decomposition

8.5.1 BCNF Decomposition

算法步骤如下：

  • 找出non-BCNF子模式Ri，进一步分解；
  • 求出F在Ri上的投影和该关系的候选键；
  • Ri是non-BCNF的原因在于$\alpha \rightarrow \beta$中$\alpha$并不是superkey。
  • 将Ri中分解成2部分，公共属性$\alpha$，其中$\alpha\rightarrow \beta$单独组成BCNF模式

Note: to determine whether or not Ri is in BCNF, the restriction of F to Ri and the candidate keys of Ri should be computed !!! 在分解出新的Ri以后，首先求出F在Ri上的投影和该关系的候选键，然后再用算法进行判断

8.5.2 3NF Decomposition

  • Functional dependencies can be checked on individual relations without computing a join.
  • There is always a lossless-join, dependency-preserving decomposition into 3NF.

Note:

  • All candidate keys should be founded out.
  • Only one Fc should be computed at first

如何用SQL语句表达、测试函数依赖?

  1. 先分组再count，但无法找出不符合函数依赖的元组
select b
from r
group by b
having count(distinct c) > 1
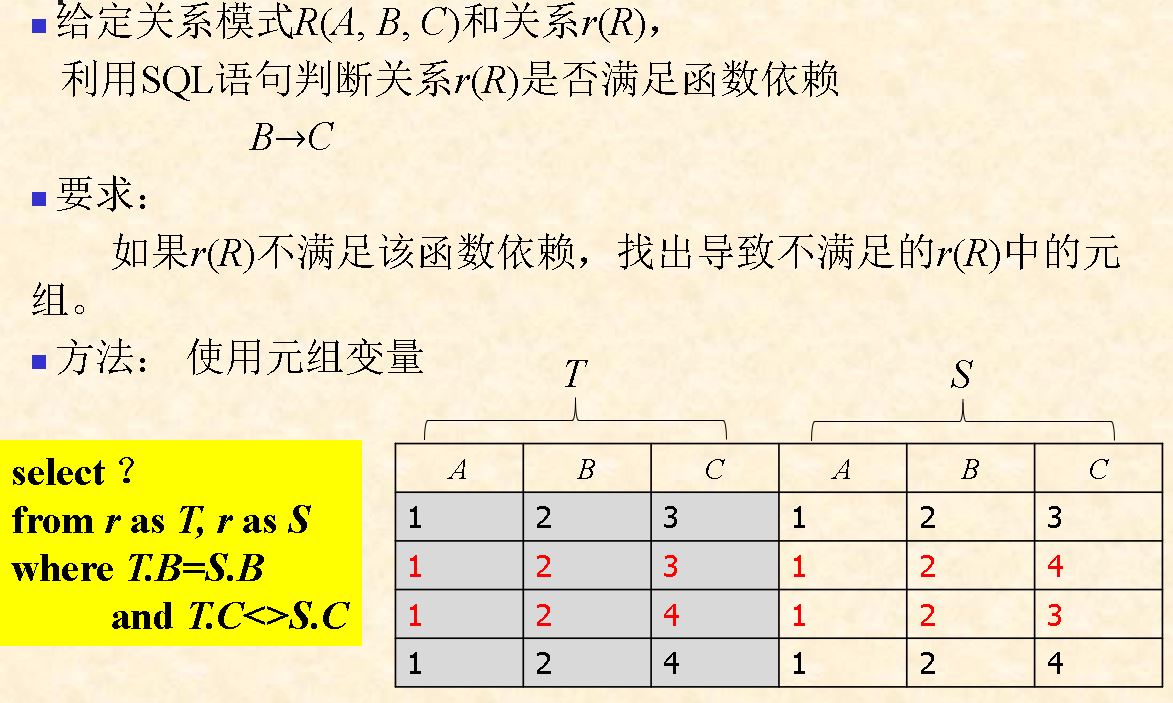
  1. 利用两表查询的方式
select ?
from r as T, r as S
where T.B == S.B and T.C <> S.C

8.5.3 Computing of Candidate Keys

  1. 将R的所有属性分为四类： L类：仅出现在F中函数依赖左部的属性 R类：仅出现在F中函数依赖右部的属性 N类：在F中函数依赖左右两边均未出现的属性(该属性一定为候选键) LR类：在F中函数依赖左右两边均出现的属性

  2. X_set代表L、N类，Y_set代表LR类

本章练习题：

  1. 给定关系表r(R)和若干函数依赖，判断r是否满足函数依赖 运用SQL语句
  2. 判断关于函数依赖的一些公式是否成立： Armstrong Axiom
  3. 求候选键
  4. 求属性闭包
  5. 求函数依赖集F的最小正则集
  6. 给定关系模式R和定义在R上的函数依赖集F，判断R属于第几范式
  7. 判断一个模式分解是否为无损连接、函数依赖保持
  8. 3NF、BCNF范式分解