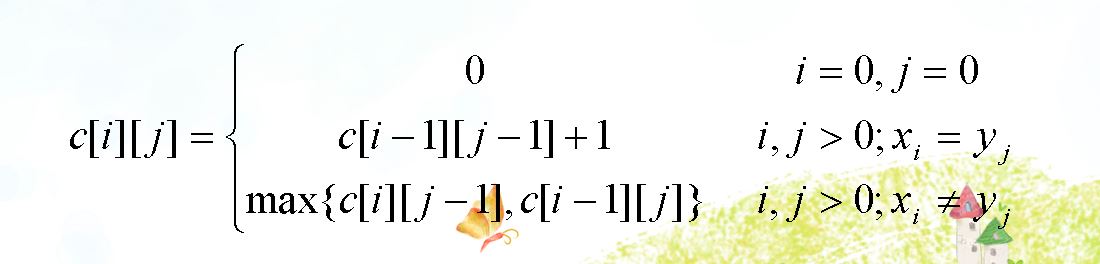Dynamic Programming
Chapter 3 Dynamic Programming
I. 基本思想
- 聪明的遍历方法
- 为全遍历,不同于贪心算法的单一路径
- 关键:==自底向上==
- 寻找最优子结构: ==该问题的最优解包含着其子问题的最优解== 验证方法:反证法
- 建立递推关系
II. 矩阵连乘问题
最优解 == 以最少的数乘次数计算出矩阵连乘的乘积
- 引子想法:改进分治法
原本的分治法:
通过递归树,可以发现在递归中经常会重复计算:
思路是将重复计算的部分存储进二维数组之中,这种方法是基于分治法的改进方法
int LookupChain(int i,int j)
{
if (m[i][j] > 0)
return m[i][j];
if (i == j)
return 0;
int u = LookupChain(i,i) + LookupChain(i+1,j) + p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++) {
int t = LookupChain(i,k) + LookupChain(k+1,j) + p[i-1]*p[k]*p[j];
if (t < u) {
u = t;
s[i][j] = k;
}
}
m[i][j] = u;
return u;
}
- 动态规划法 动态规划先从最小的子问题开始计算,==自底向上==进行合并运算。这种方法不需要递归,而且也可以避免重复计算。 (1) 分析最优子结构 原问题的最优解可以由子问题的最优解解决,对于动态规划问题,首先需要证明该问题==满足最优子结构性质==(利用反证法)
矩阵连乘问题符合最优子结构的证明: 假设$A[i:j]=A[i:k]+A[k+1:j]$是最小的计算量,且有$A[i:m]+A[m+1:j] < A[i:k]+A[k+1:j]$,则可以发现原$A[i:j] < A[i:m]+A[m+1:j]$,此时不满足假设条件,矛盾!
(2)建立递归关系

void MatrixChain(int *p,int n,int **m,int **s)
{
for (int i = 1; i <= n; i++)
m[i][i] = 0;
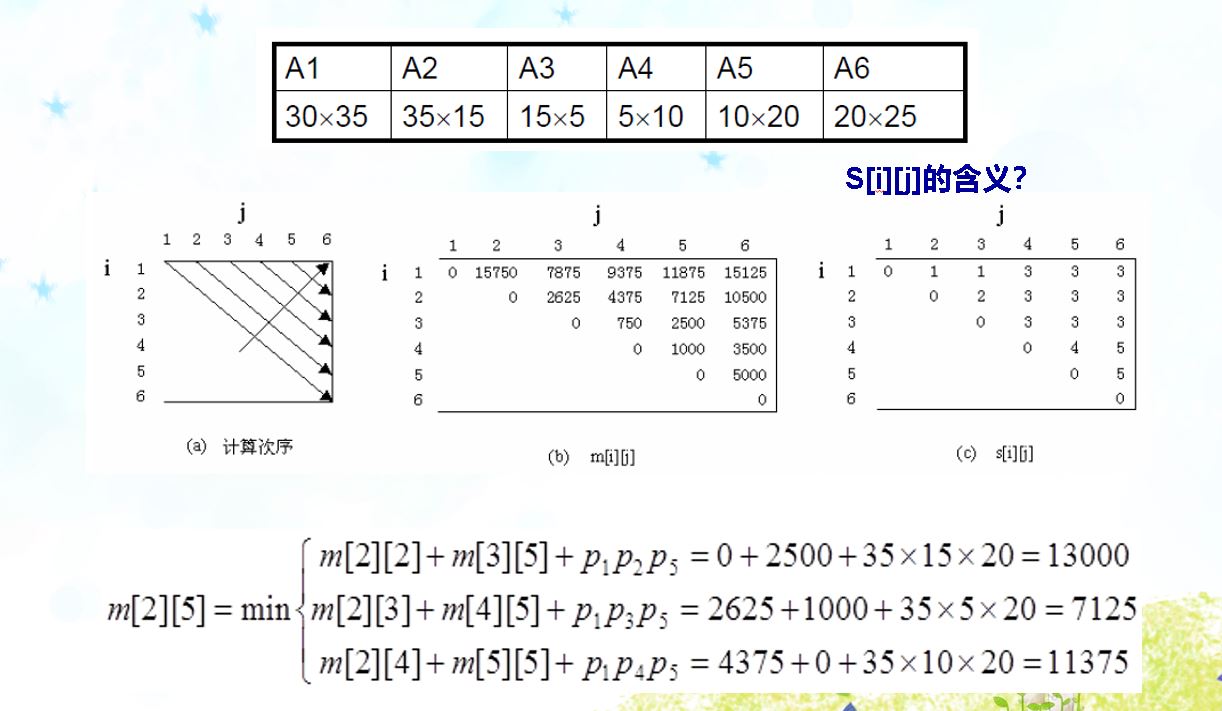
for (int r = 2; r <= n; r++) // r代表了对角线,如图a
for (int i = 1; i <= n - r + 1; i++)
{ //代表了对每条对角线的数值
int j = i + r - 1;
m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++)
{
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
接下来需要从S[i][j]矩阵中得到加括号的方案:
void trace(int i, int j, int **s)
{
if(i == j)
return;
trace(i, s[i][j], s);
trace(s[i][j]+1, j, s);
}
III. 最长公共子序列
问题描述: 给定两个序列:X={ x1, x2, …..,xm},Y={ y1, y2, ……,yn} 找出X和Y的一个最长公共子序列。
划分最优子结构: 利用从后向前考虑的突破口
建立递归结构 用c[i][j]记录序列和的最长公共子序列的长度
代码
void LCSLength(int m,int n,char *x,char *y,int **c,int **b)
{
int i,j;
c[0][0] = 0;
for (i = 1; i <= m; i++) c[i][0] = 0;
for (i = 1; i <= n; i++) c[0][i] = 0;
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++) {
if (x[i]==y[j]) {
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
else if (c[i-1][j]>=c[i][j-1])
//此处有问题
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else {
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
- 扩展:求最长上升子序列
void LIS(int a[], int b[], int n)
{
int c[n][n], d[n][n];
for(int i = 0; i < n; i ++)
b[i] = a[i];
quickSort(a, 1, n);
LCSLength(n, a, b, c, d);
}
- 扩展:利用最长公共子序列求解回文词的构造问题 解决思路:首先将给定的字符串 X 翻转得到它的逆串 Y,然后求 X 与 Y 的最长公共子序列,那么 X 的字符个数 n 减去最长公共子序列的长度即为将 X 变成回文串时最少需要添加的字符个数。
IV. 最大子段和
代码:
int maxSum(int n, int *a)
{
int sum = 0, b = 0;
for(int i = 1; i <= n; i++)
{
if(b > 0)
b += a[i];
else
b = a[i];
if(b > sum)
sum = b;
}
}
V. 凸多边形最优三角剖分
VI. 0-1背包问题
利用等长向量来表示状态