Chapter 1

I. 算法及算法复杂度

1. Definition

Input
Output
Definiteness
Finiteness
Effectiveness

note: program vs algorithm program: A program is written in some programming language, and does not have to be finite. algorithm: An algorithm can be described by human languages, flow charts, some programming languages, or pseudo-code.

2. 算法的评价

正确性
健壮性
复杂性
- 时间复杂度
- 空间复杂度
可读性
简单性

II. 算法复杂度分析

1. 指标

平均时间复杂度
最坏时间复杂度

2. 渐进性复杂度分析

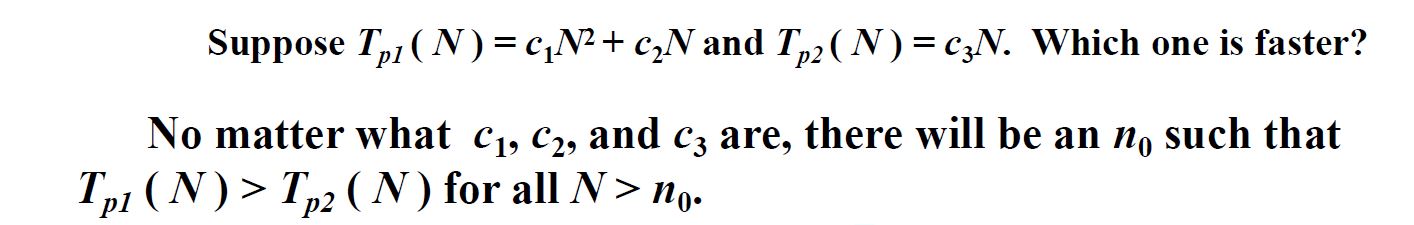
基于渐进性原理，可以对两个算法复杂度进行分析。对于求出算法的复杂度，只要求出算法的阶，便可以确定其复杂度。

Asymptotic Notation

此处对于各种阶的形象描述，请看PPT对应内容大多数情况下，我们分析算法是用大O阶，少数情况用大$\Omega$阶

3. 递归方程渐近阶的求解

(1) 代入法

对递推关系式估测一个上限，再用数学归纳法证明其正确(高手使用)

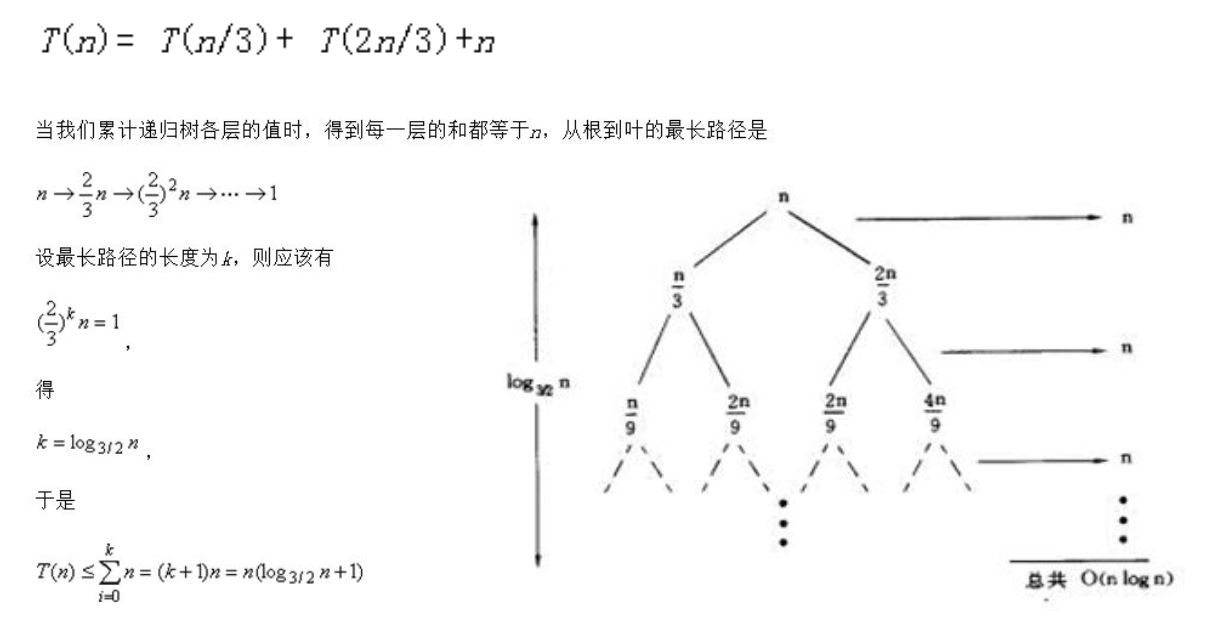
(2) 迭代法 — 较为常用

画图方法

(3) 套用公式法

该方法非常不常用，因为有很多的限制条件！！！

(4) 用特征方程解递归方程 — 考点

解题原理： 1）求解特征方程的根，得到递归方程的通解 2）利用递归方程初始条件，确定通解中待定系数，得到递归方程的解
考虑2种情况： 1）特征方程的k个根不相同 2）特征方程有相重的根

4. 证明阶关系 — 考点

利用$O$阶及$\Omega$阶的定义来进行证明：

Chapter 2

I. Divide and Conquer

Balancing 平衡子思想：尽量划分成两个规模相同的子问题

1. Binary Search Code

int binarySearch(int a[], int x, int n)
{
    int left = 0, right = n-1;
    while(left <= right)
    {
        int middle = (left + right) / 2;
        if(a[middle] == x)
            return middle;
        else if(a[middle] < x)
            left = middle + 1;
        else
            right = middle - 1;
    }
    return -1;
}

分析：算法复杂度：$O(logn)$

之所以可以减少复杂度，是由于在每次划分完子问题之后，我们只对一个子问题进行求解，不去处理另一个子问题(抛弃)，所以会效率会更高。

思考题：利用分治法求出数组的最大值和最小值

结束条件：
- 若子数组长度为1，则该子问题的最大最小值已然确定；
- 若子数字长度为2，则该子问题的最大最小值可以一步确定下来；
递归过程：将数组分成左右两个部分，分别得出左边和右边的最大最小值，然后进行比较得出哪个最大值更大，哪个最小值最小。
代码部分：

void findMaxandMin(int a[], int left, int right, int &max, int &min)
{
    if(left == right){
        min = a[left];
        max = a[right];
        return ;
    }
    else if(left + 1 == right){
        if(a[left] > a[right]){
            min = a[right];
            max = a[left];
        }
        else
        {
            min = a[left];
            max = a[right];
        }
        return ;
    }
    else
    {
        int left_min, left_max, right_min, right_max;
        int mid = (left + right) / 2;
        findMaxandMin(a, left, mid-1, left_min, left_max);
        findMaxandMin(a, mid, right, right_min, right_max);

        if(left_min > right_min)
            min = right_min;
        else
            min = left_min;
        
        if(left_max > right_max)
            max = left_max;
        else
            max = right_max;
    }
}

2. 大整数乘法

3. Strassen 矩阵乘法

4. 排序

评价排序的标准：
- 稳定性
- 复杂度
直接插入排序

void insertSort(int a[], int n)
{
    for(int i = 0; i < n; i++)
    {
        int temp = a[i];
        int j = i-1;
        while(j >= 0 && temp < a[j])
        {
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = temp;
    }
}

归并排序
- 稳定排序

//垃圾版
//渐进O(nlogn)
void mergeSort(int a[], int left, int right)
{
    if(left != right){
        int mid = (left + right)/2;
        mergeSort(a, left, mid);        //这个过程有必要吗？
        //当然是没必要把n个元素的数组划分为n个只有1个元素的数组
        mergeSort(a, mid+1, right);
        merge(a, left, mid, right);
    }
}

//升级版
//真正的O(nlogn)

void merge(int a[], int b[], int left, int mid, int right)
{
    int i = left, j = mid + 1, k = 0;
    while(i <= mid && j <= right){
        if(a[i] <= a[j])
            b[k++] = a[i++];
        else
            b[k++] = a[j++];
    }
    if(i > mid){
        for(int m = j; m <= right; m++)
            b[k++] = a[m];
    }
    else{
        for(int m = i; m <= mid; m++)
            b[k++] = a[m];
    }
}

快速排序

int partition(int A[], int p, int q)
{

}

void quickSort(int A[], int p, int r)
{
    if(p < r){
        q = partition(A, p, r);
        quickSort(A, p, q-1);
        quickSort(A, q+1, r);
    }
}

复杂度分析：
- 最坏时间复杂度：退化成插入排序，$O(n^2)$
- 平均时间复杂度：$O(nlogn)$

5. 应用

最小线性表选择 利用快速排序的Partition函数，通过中间值来寻找第k小元素。

int partition(int A[], int p, int q)
{
    //快排的partition
}
void search(int A[], int p, int r, int k)
{
    int mid = partition(A, p, r);
    int i = mid - p + 1;            //得算一下距离
    if(k > i)
        search(A, mid+1, r, k-i);
    else
        search(A, p, mid, k);
}

若想在线性的时间内$O(n)$的时间内完成算法，需要让每一次Partition的返回值尽量在Pivot位置。下面是改进的思路：

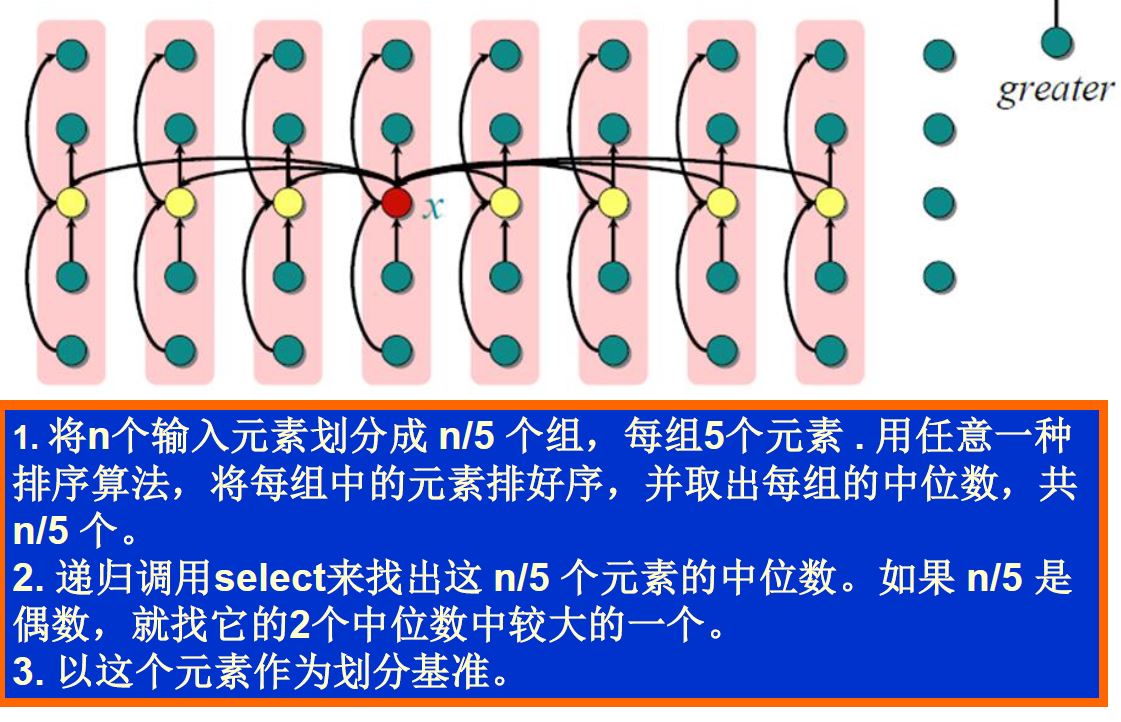
最接近点对问题

问题提出：给定平面上n个点找其中的一对点，使得在n个点的所有点对中该点对的距离最小。
分治法的思路
1. 划分成子规模点集 S1 和 S2
2. 找到 S1 和 S2 的最小距离 d。
3. 合并 S1 和 S2 ：并利用 d 在 S1 的 (md,m 和 S2 的 m,m+d 中找最大点和最小点，即 p3 和 q3 。选出最小距离，完成合并

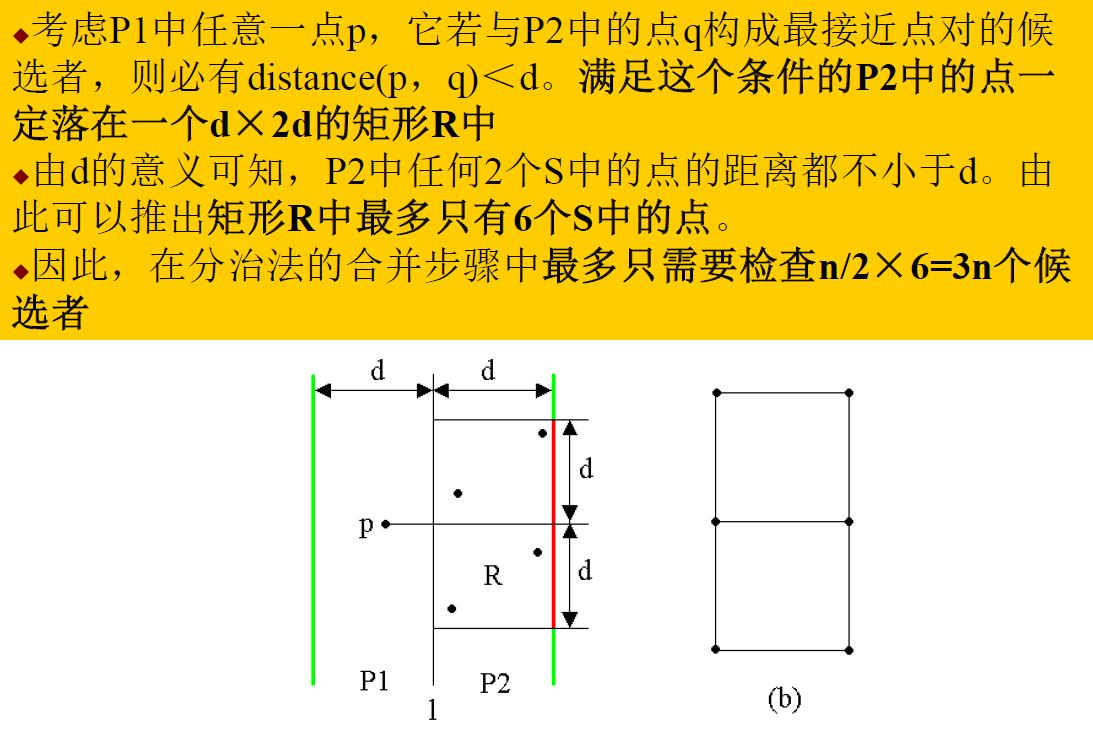
对于二维平面的时候，一维空间的合并方法不再适用，下面是二维空间的合并方式：

伪代码如下所示：

Brandon Zhang

Complexity & Divide and Conquer